La trigonometría
Introducción
La trigonometría se utiliza en muchos ámbitos de la investigación, de la ingeniería y de la técnica.
Las unidades de ángulos
Los argumentos de las funciones trigonométricas de Excel se expresan en radianes (abreviatura rd.). Las demás funciones que se suelen emplear en la práctica son:
-
Los grados GMS (grados, minutos, segundos): 43° 54’ 25.03", corresponde a la notación clásica de los cartógrafos.
-
Los grados decimales: 48,67489 más simples de introducir en un GPS.
-
Los grados, utilizados por los geómetras topográfos.
La medida de la circunferencia de un círculo corresponde a 2π radianes, es decir 360° o 400 grados. El número π se obtiene con Excel mediante la función PI().
Las dos imágenes siguientes resumen las principales funciones de conversión de una unidad a otra.
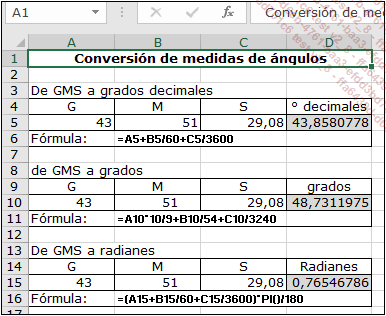
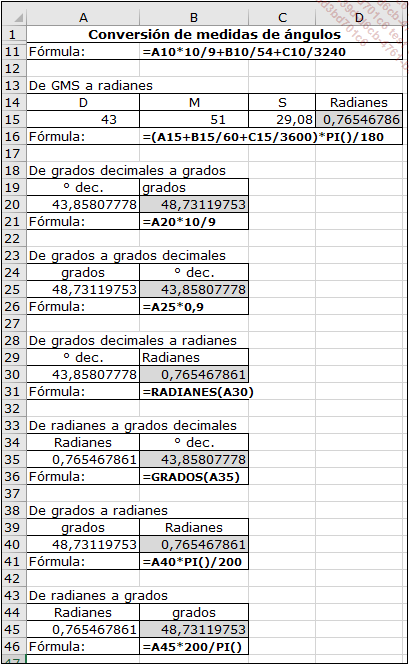
Las conversiones hacia los grados GMS requieren la redacción de funciones personalizadas VBA (véase capítulo Crear sus propias funciones).
Las funciones trigonométricas
La siguiente tabla recopila las funciones trigonométricas y las funciones correspondientes de Excel.
|
Función trigonométrica |
Función Excel |
|
Sen(x) |
=SENO(radianes) |
|
Cos(x) |
=COS(radianes) |
|
Tan(x) |
=TAN(radianes) |
|
ArcSen(x) |
=ASENO(valor) |
|
arcCos(x) |
=ACOS(valor) |
|
arcTan(x) |
=ATAN(valor) |
Las dos siguientes imágenes presentan los resultados de cálculos trigonométricos clásicos y las fórmulas empleadas.
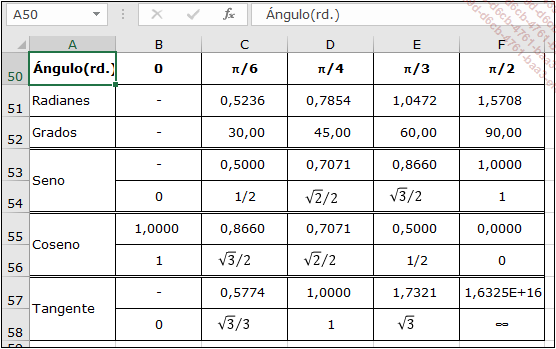
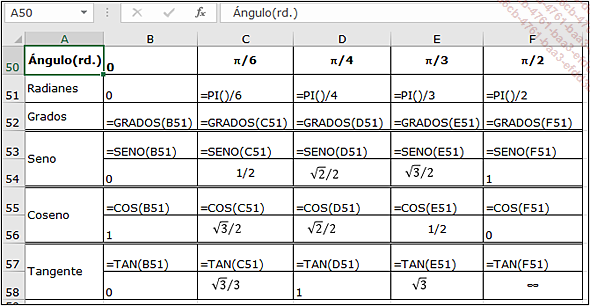
La resolución de triángulos
La resolución de triángulos es una técnica utilizada en los ámbitos topográficos. El siguiente triángulo se utiliza en los ejemplos siguientes:
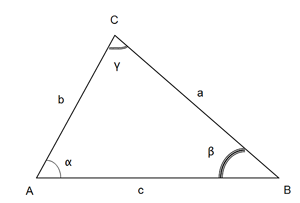
Cálculo de los ángulos (α,β,γ) del área S conociendo sus 3 lados (a,b,c)
Se utilizan las siguientes fórmulas:
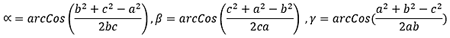
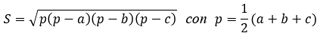
Los resultados se calculan en grados decimales para los ángulos, en m² para el área S y en metros para el semiperímetro p.
Para el ejemplo, se utilizan las siguientes dimensiones: a=70 m, b=60 m y c=80 m.
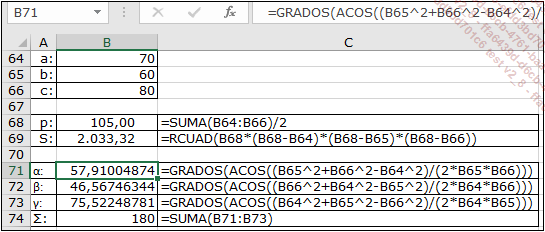
El contenido de la celda B74 permite verificar que la suma de los ángulos del triángulo es igual a 180°.
Cálculo de los ángulos α y β, del área S y del lado c conociendo γ, a y b (un ángulo y los dos lados adyacentes conocidos)
Las fórmulas son las siguientes:
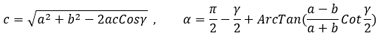
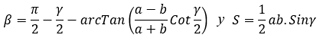
En las fórmulas del ejemplo siguiente, los ángulos se expresan en grados decimales.
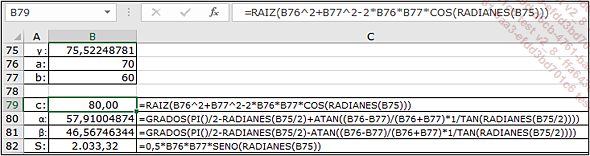
El valor del ángulo γ, expresado en grados decimales en la celda B75, se debe transformar mediante la función RADIANES para que sirva de argumento en las funciones trigonométricas SENO, COS y TAN.
La cotangente se calcula como la inversa de la tangente.
Cálculo de los lados a y b, del ángulo γ, del área S conociendo α, β y el lado c (dos ángulos y el lado común...
Aplicación en topografía
Cálculo de la altura de un punto inaccesible
Queremos calcular el desnivel H de un punto inaccesible a partir de las medidas de los ángulos α y β realizadas en una superficie supuestamente plana. El esquema es el siguiente:
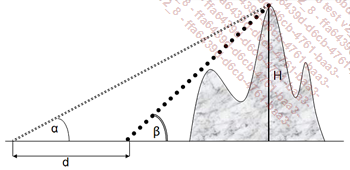
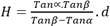
y con Excel:
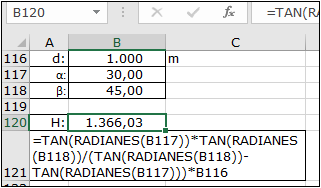
Agrimensura (cálculo de la superficie de un terreno)
El terreno se parece a un polígono cualquiera. El agrimensor procede mediante el desglose de la superficie en triángulos.
En el esquema siguiente, el agrimensor instala su teodolito en el punto T1 (a continuación, volverá a realizar la maniobra en el punto T2). Colocará piquetes en los distintos vértices del polígono (A, B, C, D, E, F, G). A continuación, medirá con la cadena de agrimensor las distancias (a, b, g, f, h) y (c, d, e, j). La medida j no es indispensable. Desde el punto T1 mide los ángulos BT1A, AT1G, etc.
El cálculo de la superficie de cada triángulo se obtiene mediante la fórmula:
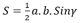 y la longitud
del lado opuesto mediante:
y la longitud
del lado opuesto mediante: 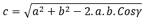 donde a y b son las longitudes de los lados
de un ángulo γ y c, la longitud del lado opuesto. Gracias a estas fórmulas,
se puede calcular la superficie y el perímetro del terreno.
donde a y b son las longitudes de los lados
de un ángulo γ y c, la longitud del lado opuesto. Gracias a estas fórmulas,
se puede calcular la superficie y el perímetro del terreno. 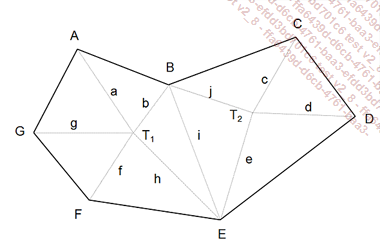
El ejemplo siguiente presenta el cálculo de la superficie y del perímetro del terreno esquematizado por el polígono.
Los resultados...
Astronomía: determinación de la posición de una estrella
El problema de la determinación de la posición de una estrella en la esfera celeste a partir de la posición del observador, depende de la rotación de la Tierra. La posición de la estrella es fija (por lo menos con respecto a la vida de un humano), mientras que la del observador es variable.
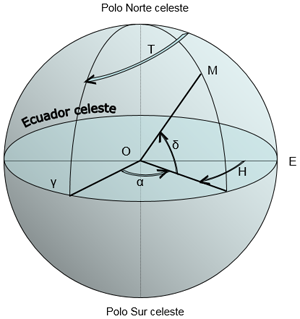
El punto de observación se constituye como sigue (véase el esquema siguiente):
-
El observador se encuentra en el punto O, en la superficie de la Tierra. El punto E corresponde al meridiano del lugar de observación (la dirección Norte-Sur).
-
La estrella observada se encuentra en M de la esfera celeste.
-
El ecuador celeste es la intersección del plano tangente a la Tierra en O con la esfera celeste.
-
El punto γ es el punto vernal, origen de las longitudes celestes.
-
El ángulo H es el ángulo horario de la estrella.
-
El ángulo T (variable) es el ángulo horario del punto γ. También se le llama "tiempo sideral local" pero es un ángulo.
-
El ángulo α (fijo) es la ascensión recta de la estrella.
-
El ángulo δ (fijo) es la declinación de la estrella.
En resumen, la posición absoluta de una estrella se caracteriza por su ascensión recta α y su declinación δ.
Ejemplo:
Sirio, la estrella más brillante (con excepción...
 Ediciones ENI Editorial | líder en informática
Ediciones ENI Editorial | líder en informática