Las herramientas de análisis de escenarios
Introducción
Excel propone una primera técnica, simple, en materia de análisis de escenarios: buscar objetivos. Se trata de partir de un resultado determinado y buscar el valor de la variable que permite obtener ese resultado. En muchos casos, esa técnica es suficiente para responder a problemas frecuentes de gestión simple.
En casos más complejos, Excel propone un complemento importante, el Solver, que permite obtener el objetivo a partir de varias variables así como de la optimización de funciones económicas como aumentar una ganancia o reducir un presupuesto.
Las ecuaciones de una incógnita: buscar objetivos
Para abrir el cuadro de diálogo de buscar objetivos, haga clic en la pestaña Datos, después en el botón Análisis de hipótesis - Buscar objetivo del grupo Previsión.
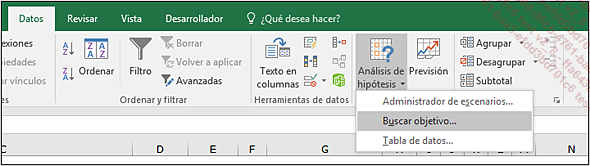
Aparecerá el cuadro de diálogo Buscar objetivo:
Las zonas de escritura de este cuadro de diálogo son las siguientes:
-
Definir la celda: celda que contiene obligatoriamente una fórmula, en la que se deberá obtener el valor objetivo.
-
Con el valor: valor deseado para la celda objetivo.
-
Cambiando la celda: celda de escritura que interviene, directamente o en cascada, en la fórmula de la celda a definir.
Ejemplo 1:
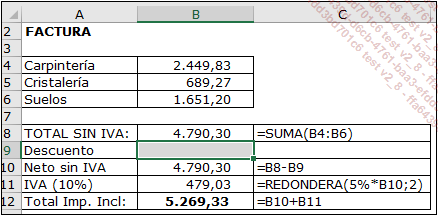
Una casa de reformas presenta a un cliente una factura final de un trabajo que acaba de realizar. El importe de la factura (5.238,09 €) supera el presupuesto inicial (5.000 €); el cliente pide que el importe facturado sea igual al importe del presupuesto que firmó. Para satisfacerle, se decide aplicar un descuento al importe sin impuestos, para obtener el importe inicial de 5.000 € IVA incluido previsto en el presupuesto. Por lo tanto, hay que averiguar ese descuento.
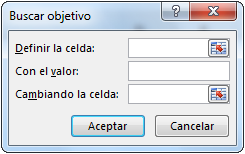
Pestaña Datos - grupo Previsión, haga clic en el botón Análisis de hipótesis y luego en Buscar objetivo.
Complete el cuadro de diálogo como en el ejemplo siguiente:
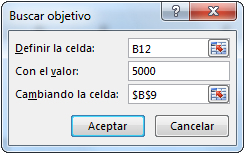
El valor de 5.000 € se define en la celda B12. Para...
Las ecuaciones de varias incógnitas: el Solver
Activar el Solver
El Solver es un producto que forma parte de los Complementos Excel (ex "macros complementarios"). Es posible que no figure en la lista de pestañas predeterminadas propuestas por Excel. Por lo tanto, es necesario activarlo previamente. Proceda de la manera siguiente:
Haga clic en la pestaña, Archivo, botón Opciones.
En el cuadro de diálogo que aparecerá, haga clic en la ventana de la izquierda, en Complementos.
Seleccione la opción Complementos de Excel de la lista desplegable en la parte inferior izquierda y haga clic en el botón Ir...
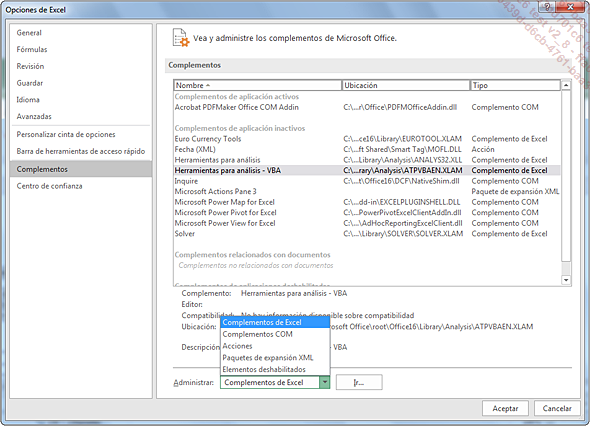
Aparecerá un nuevo cuadro de diálogo:
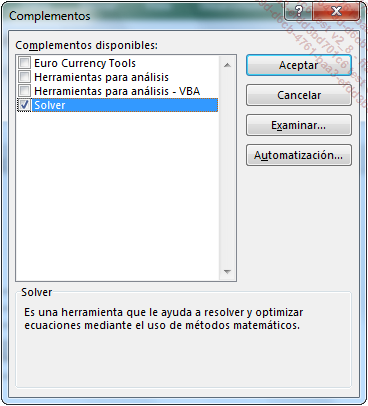
Marque la casilla Solver y haga clic en Aceptar.
El grupo Análisis, que contiene el botón Solver, aparecerá ahora a la derecha de la pestaña Datos.

Buscar un objetivo a partir de varias variables
La primera aplicación posible del Solver Excel es la determinación de un valor calculado a partir de varias incógnitas. Se trata de la técnica que hemos visto en el apartado anterior.
Ejemplo:
Un proveedor ha emitido a uno de sus clientes un gran número de facturas por varios servicios. Se ha realizado un pago por parte del departamento de Contabilidad de Proveedores del cliente, sin indicar las facturas pagadas. Para el seguimiento de los pagos, es necesario que el proveedor sepa de qué...
Optimizar mediante el Solver
El Solver es una herramienta aún más eficaz en los problemas de optimización. Permite aumentar o reducir una función económica teniendo en cuenta las restricciones técnicas y las posibles restricciones matemáticas. Los siguientes ejemplos muestran la resolución de algunos problemas clásicos de programas lineales.
La reducción de un coste de producción
Problema planteado: el director de una emisora de radio quiere reducir el coste de producción total de una franja horaria de 30 min (de 11h a 11h30), respetando la política general de la emisora que le impone una serie de restricciones. La franja horaria debe tratar noticias locales, nacionales, deportes e información meteorológica.
Queremos calcular cuántos minutos de la franja horaria deberían dedicarse a cada tema, sabiendo que:
-
10 min están destinados a la publicidad. Por lo tanto, quedan 20 min para repartir.
-
Al menos el 15% (3 min) del tiempo disponible debe centrarse en las noticias locales.
-
La duración dedicada a las noticias debe ser un tiempo al menos igual al 50% de la duración de la emisión (10 min).
-
El tiempo dedicado a la información meteorológica debe ser inferior o igual al tiempo dedicado al deporte.
-
El tiempo dedicado al deporte no debe superar el tiempo de las noticias.
-
Al menos el 20% del tiempo debe dedicarse a la información meteorológica.
-
Los costes de producción por minuto son de 300 € para las noticias locales, 200 € para las noticias nacionales, 100 € para la información meteorológica y el deporte.
Formalización: llamemos L, N, D y T a las variables que representan las duraciones de las noticias locales, nacionales, deportivas y meteorológicas. La función económica es el coste de producción total:
Coste = 300.L + 200.N + 100.D + 100.T
Y las restricciones funcionales:
-
L + N + D + T = 20
-
L >= 3
-
L + N >= 10
-
T <= D
-
D <= (L + N)
-
T >= 4
Añadamos también la restricción matemática: L, T, D, N >=0, ya que una duración no puede ser negativa. Finalmente, tendremos 7 restricciones.
Preparación de Excel: el problema requiere dos cálculos intermedios, ya que el solver no acepta fórmulas en las restricciones. En el extracto siguiente, la celda E51 contiene...
 Ediciones ENI Editorial | líder en informática
Ediciones ENI Editorial | líder en informática