Ediciones ENI Editorial | líder en informática
Los números complejos
Repaso de los números complejos
La forma clásica de un número complejo es:
Z = a + i.b
a es la parte real y b la parte imaginaria con i2 = -1. Hay que señalar que los electricistas adoptan la forma Z = a + j.b, ya que tradicionalmente "i" se reserva a la intensidad de corriente.
Las demás formas posibles son:
-
la forma trigonométrica: Z = ρ(Cosθ + i.Sinθ)
-
la forma exponencial: Z =ρeiθ
ρ es el módulo, θ el argumento. Las relaciones con la forma clásica son las siguientes:
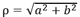.La siguiente imagen muestra una representación geométrica de los números complejos.
El conjugado de Z es Z’ = a - i.b. Las operaciones que podemos realizar con los números complejos son similares a las que se realizan con los números reales: suma, diferencia, producto, división, potencia, exponencial, etc.
Las funciones de Excel de los números complejos
Con Excel 2016, los números complejos son parte integrante de los contenidos de las celdas. A la hora de introducir los datos, basta con escribir un contenido textual del tipo a+ib (o a+jb) en una celda para que el contenido se pueda reconocer posteriormente como un número complejo válido. Del mismo modo, para utilizar un número complejo fijo como argumento de una función, basta con escribirlo entre comillas, como cualquier texto.
Si la parte real (a) es negativa, hay que empezar la introducción directa del número por un apóstrofo (’).
¡Atención! No se pueden mezclar las notaciones "i" y "j" en una misma operación.
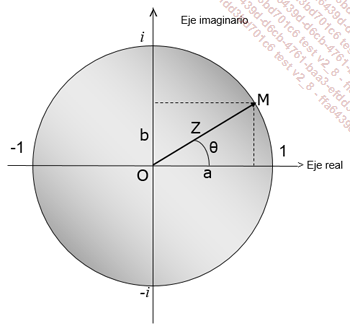
La función COMPLEJO permite construir un número complejo a partir de sus partes real e imaginaria. La sintaxis es la siguiente:
=COMPLEJO(parte real;parte imaginaria;notación)
El argumento notación es igual a "i" o "j". Si se ignora, se escogerá la notación corriente "i".
El siguiente extracto de la hoja de Excel presenta algunos ejemplos de notación de números complejos:
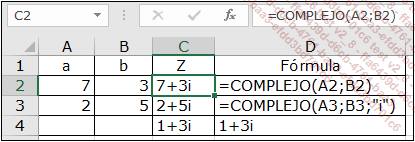
Y aquí otro ejemplo de notación trigonométrica (el ángulo escogido en B8 es π/6 es decir, 30 grados):
En la tabla siguiente, se recopilan las distintas funciones de Excel 2016 relativas a los números complejos.
|
Operación... |
Los números complejos en geometría
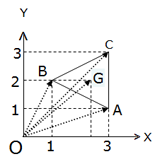
Los números complejos se aplican a muchos problemas de geometría plana asociando a un vector OM de coordenadas (a, b) el número complejo Z = a + i.b, que es el afijo del vector OM (o del punto M), siendo el punto O el origen de las coordenadas de un sistema ortogonal.
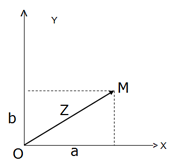
se escribe: ZAB = ZB-ZA. En el caso de la figura siguiente, el vector 
tiene como afijo ZA = 3+i y el vector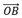 
, ZB = 1+2i.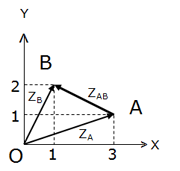
El cálculo ZAB = ZB - ZA se realiza mediante la función IM.SUSTR y como resultado da: ZAB = -2 + i.
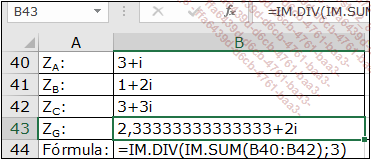
Afijo del baricentro
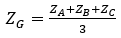
Para el ejemplo, conservemos los valores anteriores de ZA y ZB y tomemos ZC= 3 + 3i.
En la fórmula de cálculo de Excel, la función IM.SUM se emplea para sumar los 3 afijos, y después la función IM.DIV para dividir el resultado entre 3.
Homotecia
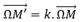.En términos de afijos de números complejos, la relación se escribe:
ZM’= ω + k (ZM - ω)
En el ejemplo de la figura siguiente, la relación k es igual a 2,5.
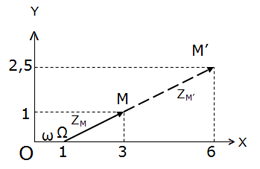
La fórmula Excel...
Los números complejos en electricidad
Los números complejos tienen mucha utilidad en los cálculos relativos a la corriente alterna sinusoidal. Una tensión sinusoidal se expresa mediante:
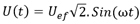
y la intensidad correspondiente mediante:
-
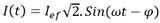
U(t): valor instantáneo de la tensión
-
Uef: valor eficaz de la tensión
-
ω: pulsación. ω=2πf donde f es la frecuencia, generalmente 50 Hz.
-
I(t): valor instantáneo de la intensidad
-
Ief: valor eficaz de la intensidad
-
φ: desfase de I con respecto a U
Expresión de la ley de Ohm en números complejos
Esta ley se expresa mediante la fórmula: U=ZI ó I = U / Z
Z es la impedancia compleja del componente o del circuito. Se mide en ohms (Ω). También empleamos los conceptos siguientes:
-
La admitancia: Y = 1/Z , medida en Siemens (Y=G + jB)
-
La conductancia: G, parte real de la admitancia
-
La susceptancia: B, parte imaginaria de la admitancia
A partir de estas fórmulas, también obtenemos los valores: I=Uef/|Z| (|Z| es el módulo de Z) y φ = Argumento(Z) si decidimos emplear la tensión compleja U en el eje de los números reales.
Para las impedancias en serie, la impedancia resultante es: Z = Z1 + Z2 + Z3 + ...
Y en paralelo: 1/Z = 1/Z1 + 1/Z2 + 1/Z3 + ...
La tabla siguiente resume las impedancias de los componentes elementales de un circuito:
|
Componente |
Impedancia compleja |
Unidad |
Observación |
|
Resistencia pura... |
