Los cálculos estadísticos
Introducción
Los cálculos estadísticos son técnicas de interpretación de datos numéricos. Estos cálculos tienen como objetivo permitir sacar conclusiones a partir de datos observados, conclusiones que escaparían a un examen puramente intuitivo.
El objetivo se alcanza en dos pasos:
La recogida de datos
Es el objetivo de la ESTADÍSTICA DESCRIPTIVA, que consiste en proporcionar indicadores simples, poco numerosos y concisos para representar una realidad física o económica.
La interpretación de los datos
Esta fase permite sacar conclusiones a partir de resultados observados de una muestra. Se trata de la ESTADÍSTICA INFERENCIAL. Para ello se utiliza el CÁLCULO DE PROBABILIDADES para definir cuál es el modelo matemático que mejor representa la realidad.
La estadística descriptiva
La estadística descriptiva trabaja por lo menos con una variable aleatoria cuyos diferentes valores se observan en una muestra de datos que representa un conjunto más vasto llamado población. Los valores observados constituyen una serie estadística.
Ejemplo 1:
Medimos el tamaño (variable aleatoria) de los alumnos de algunas clases de bachillerato (muestra) escogidos entre todas las clases de bachillerato de la región de Andalucía (población).
Ejemplo 2:
Medimos el peso unitario (variable aleatoria) de 100 paquetes de galletas (muestra), extraídos de la producción diaria (población) de una cadena de montaje.
Las funciones descriptivas básicas
Excel dispone de funciones de estadística descriptiva que son muy similares desde el punto de vista de la sintaxis:
=NOMBREFUNCION(rango de celdas)
(salvo la función CUARTIL que necesita un segundo argumento que indique el límite del cuartil escogido).
¡Atención! En el rango de celdas que sirve de argumento a la función estadística, en el cálculo solo se tienen en cuenta las celdas que contienen números. Las celdas vacías y las que contienen texto se ignoran.
El ejemplo que utilizaremos para estudiar las diferentes funciones Excel trata del tiempo de espera (expresado en minutos redondeados al más próximo) observados en una muestra de 200 pacientes...
El cálculo de probabilidades
La estadística descriptiva permite resumir una serie de datos mediante algunos indicadores característicos: la media y la desviación típica, por ejemplo. Pero es insuficiente para sacarle partido a toda la información que contiene una serie. Dos series de datos podrían tener perfectamente la misma media y la misma desviación típica, y sin embargo, ser totalmente diferentes.
El objetivo del cálculo de probabilidades es definir un modelo teórico, también llamado "ley estadística" al que se le puede destinar el reparto de datos de una serie.
Si llamamos X a la variable aleatoria que representa el tiempo de espera en urgencias, la probabilidad de que X tenga un valor determinado se expresa mediante la función f(X) que, por tanto, será la "ley de probabilidad", seguida de la variable X.
Recordemos que la probabilidad de un valor va de 0 (imposibilidad) a 1 (o 100 %, certeza).
La distribución normal (o Distribución de Gauss)
Es la más extendida ya que muchos casos prácticos aplican esta distribución: datos numerosos, valores continuos (tiempo, longitud, peso, etc.), observaciones independientes. La función f(X) se presenta bajo la forma de la típica "curva en forma de campana".
Para estudiar los ejemplos de funciones Excel que emplean la distribución normal, supongamos...
La estadística inferencial
La estadística inferencial es un conjunto de técnicas que, a partir de indicadores de la estadística descriptiva y de modelos de cálculo de probabilidades, permiten medir un riesgo, explicar una variable mediante una o varias variables, comparar muestras, validar un modelo, etc. y, por último, tomar una decisión.
Validar un modelo - La prueba χ2 de Pearson
Queremos probar la hipótesis de que el tiempo de espera en urgencias sigue una distribución normal. Para ello, calculemos cuáles deberían ser teóricamente los efectivos si su distribución siguiera la distribución normal. La tabla siguiente muestra los resultados y el modo en que se han calculado mediante la función DISTR.NORM.N que ya hemos estudiado.
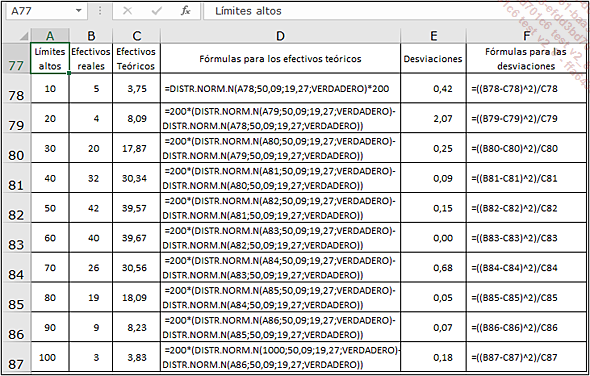
El cálculo de x2 se realiza calculando las separaciones para cada clase mediante la fórmula (Ef. Real-Ef. Teórico)²/Ef.Teórico. Los resultados se encuentran en el rango de celdas E78:E87. La x2 se obtiene totalizando esas separaciones: el resultado es 3,96 en la celda E89.
Comparemos ese resultado con el resultado de la función de Excel INV.CHICUAD.CD. Esta función tiene como argumento una probabilidad y corremos el riesgo de equivocarnos (tomamos un umbral clásico del 5%) y un número de grados de libertad igual a (número de clases-3), es decir, 7 en nuestro caso.
El resultado es el siguiente:

Ya que el x2 calculado (3,96) es menor que x2, podemos sacar la conclusión de que el modelo de la distribución normal puede aplicarse sin problemas a la variable X (tiempo de espera), con un 5% de riesgo de error.
Explicar una variable
El principio consiste en determinar en qué medida una variable Y se explica mediante una variable X (regresión simple) o mediante varias variables X1, X2, ..., Xn (regresión múltiple) y, en un segundo paso, validar la legitimidad de esta relación.
Generalmente, nos solemos conformar con las regresiones lineales, también llamadas ecuaciones Y = a.X+b para la regresión simple o Y = (a1.X1 + a2.X2 +... an.Xn) + b para la regresión múltiple.
La función Excel que permite tratar las regresiones lineales es la función ESTIMACION.LINEAL, en referencia a la "línea de regresión" que es la representación geométrica...
 Ediciones ENI Editorial | líder en informática
Ediciones ENI Editorial | líder en informática