El cálculo matricial
Repaso de las matrices
Sin entrar en definiciones teóricas que se salen del tema que tratamos en este libro, consideramos que una matriz se presenta en forma de tabla rectangular de n líneas y de m columnas que contienen números reales. Cada elemento de la matriz se puede designar por su índice de línea y su índice de columna:
aij representa el número situado en la intersección de la línea i y de la columna j.
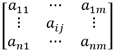
Una matriz con el mismo número de líneas y de columnas es una matriz cuadrada.
Suma de matrices: las matrices con las mismas dimensiones pueden sumarse. Si A y A’ son dos matrices de dimensiones n x m; el elemento genérico de la matriz C = A + A’ se calcula mediante:
cij = aij + a’ij
Multiplicación por un escalar k: el resultado es una matriz de la misma dimensión cuyo elemento genérico es:
cij = k.aij
Multiplicación de dos matrices: la multiplicación de una matriz A (n líneas x m columnas) por una matriz B (m líneas x p columnas) es una matriz C de n líneas x p columnas cuyo elemento genérico es:
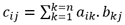
Matriz identidad (I): matriz cuyos elementos valen todos 0 excepto los elementos de la diagonal que son igual a 1.

Matriz transpuesta: la matriz transpuesta M de elemento genérico aij es la matriz M’=tM de elemento genérico aji.
Matriz invertible: la inversa de una matriz cuadrada...
Tratamiento de las matrices con Excel
Designación de matrices
La forma más simple de designar una matriz es el área rectangular de celdas localizada por su dirección o por su nombre. En el ejemplo siguiente, el rango A3:D6 (llamado M) representa una matriz.
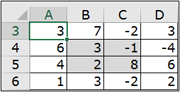
Una matriz también se puede designar en forma de constante matricial. La expresión {2.3;4.7;2.9} designa la matriz de 3 líneas x 2 columnas siguiente:
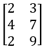
Una constante matricial se puede utilizar con esta forma en una fórmula en la que entran en juego varias matrices (suma, multiplicación, etc.). También puede usarse en forma de escritura "matricial" (véase el capítulo Consejos de buenas prácticas - Las fórmulas matriciales) para completar un rango de celdas. En el ejemplo, el rango D11:E13 se ha completado en el orden siguiente:
-
la selección del rango D11:E13
-
la escritura de la fórmula ={2.3;4.7;2.9}
-
la validación en forma matricial mediante la combinación de teclas ShiftIntro.
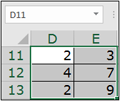
Para extraer una submatriz de una matriz de base, hay que emplear la función DESREF cuya sintaxis general permite designar cualquier área rectangular de celdas contiguas dentro de esta matriz de base
=DESREF (matriz de referencia;desplazamiento de líneas;desplazamiento de columnas;[número de líneas];[número de columnas])
Los dos últimos argumentos...
Aplicación en el álgebra lineal
Resolución de un sistema de n ecuaciones lineales con n incógnitas
La forma general de un sistema de n ecuaciones lineales con n incógnitas es:
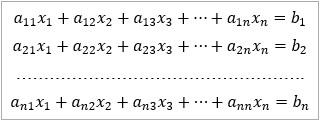
En forma matricial, el sistema se escribe: A.X = B, es decir:
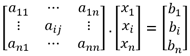
Por lo tanto, la solución se obtiene mediante la fórmula X = A-1.B, siempre y cuando la matriz A sea invertible.
Ejemplo 1:
Queremos resolver el siguiente sistema lineal de tres ecuaciones de tres incógnitas:
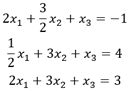
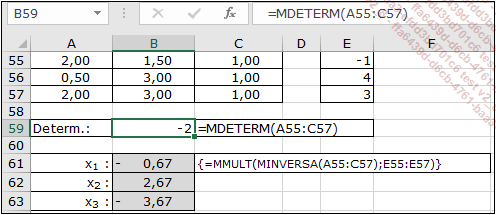
La solución del sistema viene dada mediante la escritura matricial:

Dado que el determinante es distinto de 0, la matriz es invertible.
La transcripción en Excel es la siguiente:
Diagonalización de una matriz
La diagonalización de una matriz, cuando esto es posible, permite simplificar mucho los cálculos. Una matriz M se diagonaliza si se puede escribir así: M = P-1.D.P. D es la matriz diagonal y P la matriz de paso. La matriz diagonal está compuesta por los valores propios de la matriz y la matriz P por la yuxtaposición de los vectores propios de esta misma matriz.
Los valores propios son las raíces del polinomio obtenido mediante el cálculo del determinante de la matriz [λ.I - M].
Ejemplo:
Tomando la matriz:
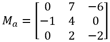
Averigüemos los valores de x tales que:
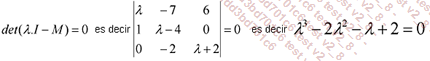
Los valores propios, raíces de este polinomio, son 1, -1 y 2.
Los vectores propios V demuestran la relación:...
Aplicación a los circuitos eléctricos de malla
Los circuitos eléctricos pueden tener forma de malla. La ley de Ohm generalizada se escribe: U + Z.I donde Z es la matriz de las impedancias. Para un cuadripolo esquematizado de la siguiente forma:

la ley de Ohm se escribe:
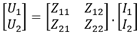
Por lo tanto, el cálculo de las intensidades se realiza mediante la inversión de la matriz de las impedancias. Esta matriz Z puede estar compuesta por impedancias complejas. A pesar de que Excel 2016 no dispone de la función de inversión de matrices complejas, es posible resolver el problema.
Descomponer las matrices Z y Z -1en partes reales e imaginarias, es decir: Z = A + j.B y Z-1= A’ + j.B’. El cálculo de A’ y B’ se realiza mediante las relaciones siguientes: A’ = (A + B.A-1.B) -1 y B’ = -A-1.B.A’.
El siguiente ejemplo de Excel se basa en una matriz Z compleja (3x3). Las matrices A y B se calculan mediante las funciones IM.REAL e IMAGINARIO. Estas funciones no funcionan en modo "matricial". Por lo tanto, hay que utilizarlas en una primera celda y después volver a copiarlas en las otras 8.
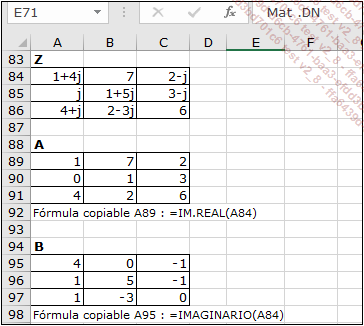
Las matrices A’ y B’ se calculan a partir de las matrices A y B mediante las relaciones anteriores. Por último, la matriz inversa de Z se vuelve a crear a partir de sus partes reales e imaginarias mediante la función COMPLEJO.
En el ejemplo siguiente, para una mejor comprensión...
Aplicación de las matrices en las rotaciones
El cálculo matricial tiene muchas aplicaciones, como en el cálculo de estructuras, en el de la ingeniería o incluso en los videojuegos para manipular las figuras geométricas y, concretamente, realizar las rotaciones.
Las rotaciones planas (2D)
Si consideramos el sistema ortonormal siguiente:
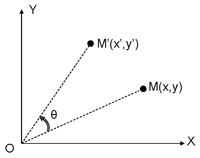
La rotación plana de origen O y el ángulo θ permite calcular la posición de un punto M’ (x’,y’) con respecto a un punto de origen M (x,y) por la matriz de rotación siguiente:
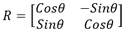
O dicho de otra forma, las coordenadas (x’,y’) del punto M’ cumplen la relación matricial:
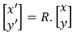
La matriz de rotación también puede aplicarse a un polígono definido por las coordenadas de sus vértices: (x1, y1), (x2, y2), ..., (xn, yn).
Por lo tanto, tendremos:
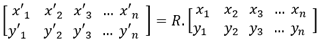
En el ejemplo siguiente, se aplica una rotación de 90°(π/2) a un rectángulo cuyos vértices tienen como coordenadas (1,1), (5,1), (5,2), (1,2).
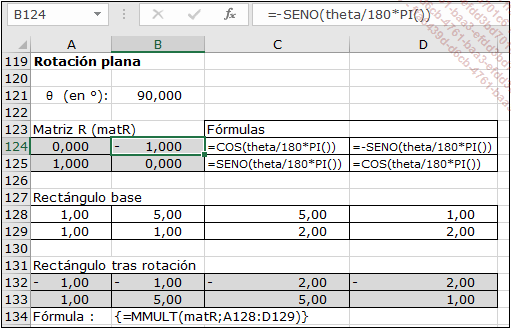
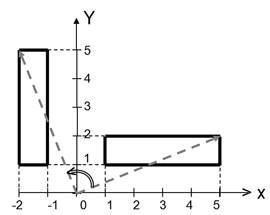
La siguiente figura permite visualizar la operación de rotación realizada.
Las rotaciones en el espacio
En el caso de las rotaciones, según las tres dimensiones, utilizamos los ángulos de Euler. Esos tres ángulos definen la rotación resultante de las tres rotaciones elementales:
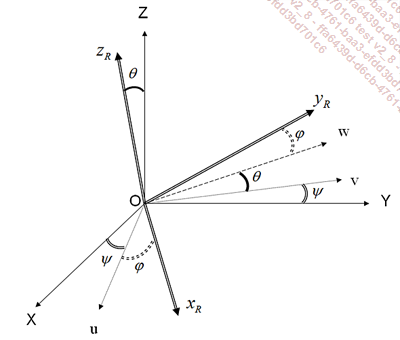
En la figura anterior, pasamos del sistema de coordenadas de referencia OXYZ al sistema...
Aplicación de las matrices en economía
La matriz de coeficientes técnicos
La tabla siguiente recopila, en moneda local, el sistema de intercambio entre los tres sectores de una economía que funciona totalmente en autarquía.
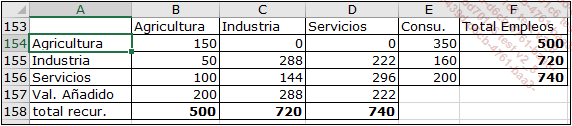
En esta tabla, la columna B, relativa a la agricultura, indica que, para ofrecer un empleo de 500, las empresas agrícolas han comprado 150 a otras empresas agrícolas, 50 a la industria y 100 a empresas de servicios.
La matriz de coeficientes técnicos se compone de números que representan los recursos necesarios para obtener 1 unidad monetaria de cada sector. Así, para obtener 1 unidad monetaria agrícola, son necesarias 150/500=0,3 unidades agrícolas, 50/500=0,1 unidades de industria y 100/500=0,2 unidades de servicios.
La matriz de los coeficientes técnicos, llamada MCT (rango B161:D163) se presenta así:
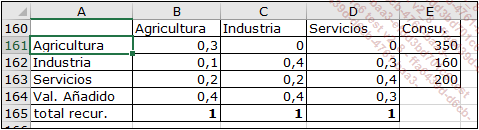
La fórmula de la celda B161, que se puede copiar en todas las demás celdas de la tabla es: =B154/B$158.
Llamemos xA, xI, xS a los recursos de cada uno de los sectores para satisfacer los consumos finales CA, CI, CS. La relación matricial siguiente se demuestra:
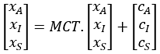 o incluso
o incluso 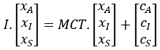 , siendo I la matriz identidad.
, siendo I la matriz identidad.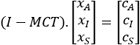 y finalmente,
y finalmente, 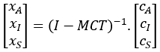 .
.Ejemplo:
Queremos conocer los recursos de cada sector necesarios para aumentar un 30% el consumo del sector "Industria", es decir, 160 x 1,3 = 208 unidades monetarias. Las funciones MMULT...
 Ediciones ENI Editorial | líder en informática
Ediciones ENI Editorial | líder en informática