Otros problemas otras soluciones
Series temporales
Cuando las observaciones evolucionan a lo largo del tiempo, las modelamos usando series temporales y comprobamos si su secuencialidad influye en los valores de las observaciones.
1. Introducción
Las series temporales tienen una variable de tiempo como variable subyacente. Podemos pensar en ellas como la extensión de una lista de observaciones, indexadas usando una variable temporal. En última instancia, si los intervalos de tiempo tienden hacia 0, la variable de tiempo discreta se puede definir como continua. En este caso, consideramos la correspondiente serie discreta como una serie de posibles observaciones de la serie continua, que muchas veces es el resultado de representar un sistema físico (una oscilación, una señal electrónica o biológica o el precio de los índices bursátiles, etc.).
El estudio de series temporales se basa en que, a priori, cada valor de la serie depende de otros valores de la serie, normalmente valores anteriores. En el último caso, tratamos naturalmente de expresar esta dependencia usando una función. Esta función se puede percibir como una función generadora de la serie, que se aplica a un conjunto de primeros elementos.
En este sentido, es comprensible que estas series también se denominen «procesos».
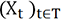 definidas en el mismo espacio de probabilidad.
definidas en el mismo espacio de probabilidad.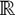 .
.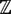 , lo que también expresa que no prejuzgamos
la existencia de un inicio del proceso. En la práctica,
restringimos T a un conjunto finito de índices I incluidos
en el conjunto de números naturales positivos
, lo que también expresa que no prejuzgamos
la existencia de un inicio del proceso. En la práctica,
restringimos T a un conjunto finito de índices I incluidos
en el conjunto de números naturales positivos 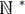 . Las observaciones se realizan entre dos momentos
del tiempo y el primero se puede indexar como «1».
. Las observaciones se realizan entre dos momentos
del tiempo y el primero se puede indexar como «1».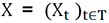 se puede
estudiar en función de varios criterios: ¿su media
móvil es constante o se puede modelar mediante una función
identificable, que exprese una tendencia? Con respecto a esta media
o función, ¿los valores residuales tienen un aspecto particular
(como una oscilación...
se puede
estudiar en función de varios criterios: ¿su media
móvil es constante o se puede modelar mediante una función
identificable, que exprese una tendencia? Con respecto a esta media
o función, ¿los valores residuales tienen un aspecto particular
(como una oscilación...Sistemas difusos
1. Introducción
Esta sección presenta conceptos que encontrará en diferentes algoritmos y paquetes. Permitirá abordar diversos temas en otros contextos, en particular el de los sistemas expertos. Estos sistemas parece que han pasado de moda más allá del mundo industrial, pero estamos convencidos de que pronto volverán a tener vigencia en las herramientas de los futuros data scientists.
El hecho de que los sistemas difusos (fuzzy systems) sean efectivos para reconocer patrones y aproximar funciones «complejas» proviene en parte de su capacidad para dar soporte a la codificación eficiente del conocimiento.
Los sistemas difusos se apoyan en sistemas expertos basados en reglas (rule-based systems), que a menudo se ven como «SI sucede esto, ENTONCES pasa eso».
Como sugiere el término «fuzzy», estas reglas también se ven empañadas por la lógica difusa (incorporando la noción de conjuntos difusos, los fuzzy set, que abordaremos a continuación).
Un conjunto difuso se puede entender como la pareja formada por un conjunto «clásico» (en inglés crisp) y una función que opera sobre los elementos de este conjunto, que recibe sus valores de un intervalo determinado, normalmente [0,1]. Esta función cuantifica la probabilidad de una afirmación (de hecho, es el nivel de pertenencia al conjunto, una extensión de la noción de «función característica» que es igual a 0 cuando un elemento no está en el conjunto y 1 cuando el elemento está en el conjunto).
La facilidad para interpretar las reglas por parte de los humanos ayuda a afinar estos sistemas, especialmente si el número de reglas se mantiene razonable. Es posible codificar el conocimiento incierto, lo que mejora el diálogo con los expertos porque no es necesario capturar todo el conocimiento de un tema a través de una única regla compleja y expresado de una sola vez. Por el contrario, se apilarán reglas unitarias con su incertidumbre, de modo que su validación individual sea sencilla. La base que contiene las reglas podrá evolucionar en incrementos sucesivos, sin desestabilizar el conjunto.
El primer inconveniente de estos sistemas es que necesitan recurrir a expertos a los que entrevistar para definir las reglas...
Enjambre (swarm)
Las analogías con la naturaleza inspiran a los creadores de algoritmos. Cuando observamos la acción de una colonia de hormigas (ant) que busca comida en un mantel durante un almuerzo en el césped, nos sorprende «la inteligencia colectiva de las hormigas». Estas se organizan en filas que se dirigen a los puntos donde encuentran más recursos, explotan el territorio de manera eficiente, cambian su comportamiento y su organización cuando añadimos obstáculos o cuando escasea un recurso en algún punto del mantel.
La idea de los algoritmos que utilizan esta analogía es sencilla: no hay inteligencia centralizada en estos comportamientos, pero la conjunción de comportamientos que son fáciles de codificar (es decir, poco inteligentes) y los intercambios de información breves determinan una cierta inteligencia colectiva del enjambre (swarm).
1. Swarm y optimización: el algoritmo PSO
El uso más común de algoritmos como estos es la búsqueda del punto óptimo en el caso de problemas muy difíciles, normalmente cuando hay varios puntos óptimos locales. Tenga en cuenta que encontrar estos puntos óptimos locales puede ser parte de nuestros objetivos, al igual que nuestras hormigas no solo buscan la mejor fuente de alimento, sino todas las fuentes de alimento importantes a las que se puede acceder a cierta distancia de su base.
a. Presentación de PSO
El algoritmo PSO (Particle Swarm Optimization) implementa una población de partículas que se mueven estocásticamente en el espacio de búsqueda. Cada individuo se caracteriza por su mejor desempeño en este espacio (por ejemplo, donde la hormiga ha encontrado más comida, y no donde realmente está la mayor cantidad de comida). El individuo comunica esta experiencia a una determinada parte de la población (en función de sus medios de comunicación y su voluntad como programador). Algunas veces es más sensato comunicar la información solo a un grupo restringido de la población, para no distorsionar el comportamiento de todo el enjambre. Esta información influye en el comportamiento del resto de los individuos informados, quienes la compararán con la información que tiene cada uno de sus interlocutores y su propia información....
 Ediciones ENI Editorial | líder en informática
Ediciones ENI Editorial | líder en informática


