Dominar los conceptos básicos
Estar en armonía con los datos
El error más común que cometen las personas recién iniciadas en data sciences es usar directamente, sin precauciones y sin un análisis preliminar, los algoritmos disponibles sobre datos mal entendidos.
A lo largo del proceso de desarrollo de su estudio y desde su primer contacto con un problema, el data scientist estará interesado en evaluar sus datos, usando diferentes herramientas estadísticas para poder visualizarlos desde varios puntos de vista. Esta es la única manera de poder formular con juicio las hipótesis que queremos validar, o no, a lo largo del proceso.
El lector interesado que quiera volver a los aspectos básicos, sin duda quedará satisfecho con el libro de Andrei Kolmogorov, a quien debemos muchas contribuciones a ciertos conceptos que subyacen a nuestra práctica de las data sciences (formalización de la lógica intuitiva como «cálculo sobre problemas», ley fuerte de los grandes números, axiomas de probabilidad a través del lenguaje de las teorías de medida, upsilon-entropía que permite calificar los estimadores, aplicación del método de Poincaré al estudio de equilibrios, etc.).
La interpretación de herramientas estadísticas requiere asimilar algunas nociones fundacionales sobre probabilidad, que vamos a abordar ahora.
1. Algunas nociones principales
a. Fenómeno aleatorio
Se enfrenta a un fenómeno aleatorio si, cuando se realiza un experimento varias veces en condiciones idénticas, se obtienen resultados diferentes (y, por lo tanto, en cierto modo, impredecibles).
Observe que, en esta definición, el hecho de que un fenómeno se identifique como aleatorio depende de la incapacidad del observador para preverlo por completo, lo que le hará declarar de forma categórica que el fenómeno es intrínsecamente aleatorio.
Sin embargo, cuando repetimos el experimento un gran número de veces, vemos que los resultados se distribuyen siguiendo una ley o distribución estables, es decir, con frecuencias de aparición de los resultados que dependen del valor del resultado. Por ejemplo, si observa las calificaciones de bachillerato de un gran número de estudiantes, encontrará una frecuencia de las calificaciones promedio más altas que la frecuencia...
Matrices y vectores
1. Convenciones, notaciones, utilización básica
La intención de esta sección es que se familiarice con el uso práctico de matrices y vectores, tal y como se presentan con gran frecuencia en este libro. El aspecto matemático subyacente no se tiene en cuenta (o poco).
Fabriquemos una matriz
Suponga un dataset formado por filas (por ejemplo, que representan eventos o individuos) y cuyas columnas representan los valores para cada atributo (en inglés feature). Dentro de una tabla con otros individuos, una fila que describa a un individuo llamado Robert, de 40 años, casado y que viva en la ciudad de París, se podría codificar de la siguiente manera:
!nombre ! edad ! estado civil ! ciudad !
! ! ! ! !
!ROBERT ! 40! C ! PARÍS !
!PHILIPPE ! 30! S ! LYON !
!RODOLF ! 20! S ! LYON !
!CASADO ! 35! C ! PARÍS ! Si memorizamos el número de fila de cada individuo:
!nombre ! fila !
! ! !
!ROBERT ! 1 !
!PHILIPPE ! 2 !
!RODOLF ! 3 !
!CASADO ! 4 ! Si codificamos el estado civil de la siguiente manera: «C» vale 1 y «S» vale 0, entonces, si reemplazamos la ciudad por su código postal, podemos obtener una matriz de cifras con el mismo significado:
! fila ! edad ! estado civil ! ciudad !
! ! ! ! !
! 1 ! 40! 1 ! 75000 !
! 2 ! 30! 0 ! 69000 !
! 3 ! 20! 0 !...Estimaciones
1. Posicionamiento del problema de estimación
a. Formulación general del problema
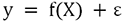 .
.En el caso actual, se desconoce un gran número de elementos del vector y se va a determinar la aplicación f(). Se supone que el vector de error tiene una media de 0 y una norma pequeña con respecto a la norma de y.
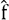 , y una estimación de y, que denotaremos
con
, y una estimación de y, que denotaremos
con 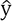 , tal que
, tal que 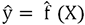 .
.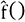 , tal que
una «forma» de desviación entre
, tal que
una «forma» de desviación entre 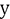 e
e 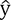 sea mínima.
sea mínima.Para expresar la desviación general que hay que minimizar, tenemos una aplicación para medir la desviación o «pérdida» (loss en inglés). La desviación se calcula entre un valor conocido y un valor estimado para una observación determinada.
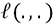 para denotar
esta aplicación que, en el caso de que yi sean valores
de
para denotar
esta aplicación que, en el caso de que yi sean valores
de 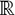 , es una aplicación
de
, es una aplicación
de 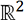 a
a 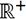 .
.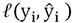 podría
tomar la forma de una distancia inducida por una norma o de una
función constante sobre
podría
tomar la forma de una distancia inducida por una norma o de una
función constante sobre 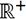 de una distancia inducida por una norma.
de una distancia inducida por una norma.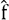 , tal que
la media de
, tal que
la media de 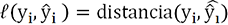 sea mínima
o que la media de sus cuadrados lo sea (observe que no
hemos definido aquí la distancia elegida).
sea mínima
o que la media de sus cuadrados lo sea (observe que no
hemos definido aquí la distancia elegida).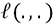 sea mínima.
sea mínima.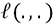 .
.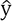 por su valor y denotando la media sobre las
observaciones del training set con < >T:
por su valor y denotando la media sobre las
observaciones del training set con < >T: 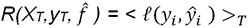
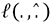 .»
.»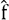 que minimice R en
las observaciones del training...
que minimice R en
las observaciones del training...Puesta en práctica: aprendizaje supervisado
Vamos a realizar un pequeño ciclo de construcción de una predicción con el fin de poner en práctica los conceptos vistos anteriormente. En primer lugar, nos vamos a equipar con un conjunto de observaciones. Este conjunto incluirá 10 000 observaciones, dos features de entrada y una para predecir. Buscaremos el modelo f, siendo y la feature objetivo y X (x1, x2), la entrada. El conjunto de observaciones Z = (X, y) se diluye en un conjunto de entrenamiento Ze de 6 000 líneas y un conjunto de validación Zv de 4 000 líneas.
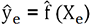 .
.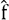 sobre el conjunto de validación Xv y
obtendremos un vector de predicciones
sobre el conjunto de validación Xv y
obtendremos un vector de predicciones 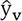 que compararemos con el vector Yv de
los valores reales, resultantes del conjunto de validación.
que compararemos con el vector Yv de
los valores reales, resultantes del conjunto de validación.Para hacer esto, vamos a crear un conjunto «ficticio» Z donde hemos impuesto, y después perturbado aleatoriamente, el hecho de que y está ubicado, más o menos, en el plano 2. x1 - 7. x2 + 1.
Nuestra esperanza es constatar que los algoritmos utilizados encuentran la ecuación de este plano, con un error de amplitud bajo.
1. Preparación
El código para crear el conjunto de observación ficticia es el siguiente (sin interés específico):
# un dataset fáctico, creación de las matrices #
rm(list=ls())
g <- function(x){s <- round(abs(sin(x)*1000 ))
set.seed(s) # randomize
# pero garantiza que g(constante) es una constante
x*(1- 0.5*rnorm(1)*sin(x))} # para perturbar
set.seed(2); x1 <- matrix(rnorm(10000))
set.seed(3); x2 <- matrix(rnorm(10000))
y <- matrix(2*x1-7*x2+1)
y <- apply(y,1,g)
Z <- data.frame(x1,x2,y)... Ediciones ENI Editorial | líder en informática
Ediciones ENI Editorial | líder en informática


