Complementos útiles
GAM: generalización de LM/GLM
Para ir más allá con el modelo lineal, vamos a estudiar su generalización, que con razón forma parte de la caja de herramientas de muchos data scientists.
El modelo aditivo generalizado (GAM) va más allá del modelo GLM en la generalización de modelos lineales, por lo que debe aprenderlo desde el inicio de su trabajo.
Es un modelo muy manejable, con grandes posibilidades, eficiente en cuanto a prestaciones, con cualidades que pueden favorecer un comportamiento de overfitting porque permite hacer lo que podríamos llamar «cosido a mano» sobre los datos. Pero también es un modelo que nos anima a comprender y analizar nuestros datos y que es muy interesante de utilizar, desde una perspectiva valiente y exploratoria.
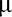 y de varianza
y de varianza 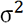 con
con 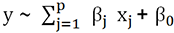 .
.En el modelo GLM se introducen otros conceptos, pero manteniendo la linealidad de los coeficientes, que son siempre los argumentos que se quiere descubrir.
En este modelo, la variable de respuesta puede no corresponder a una distribución normal, pero debe ser parte del «rango» de distribuciones de la «familia exponencial» que incluye, entre otras, las siguientes distribuciones: Normal, Multivariante Normal, Log-Normal, Gaussiano inverso, Gamma, Gamma-Normal, Gamma-inverso, Exponencial, Chi-cuadrado...
Manipulación de imágenes
La manipulación de imágenes permite extraer diferentes features de ellas o preprocesarlas antes de aplicar diferentes algoritmos (generalmente, un tratamiento a través de una red neuronal).
Vamos a abordar estas manipulaciones de una manera sintáctica y sin adornos para que pueda ir más lejos al descubrir la sencillez de las herramientas que ya tiene a su disposición.
Manipular imágenes también significa evolucionar en un mundo espacial bidimensional y tridimensional, como en la geografía, donde dos de las dimensiones son las variables que explican la tercera (intensidad, color). Otra similitud con los usos geográficos y geofísicos es que las dimensiones espaciales se deben considerar en conjunto a través de su covarianza, por ejemplo: la distancia entre dos ojos es más representativa de las características de un rostro que la distancia entre los valores de sus respectivas coordenadas.
En una imagen están ocultas, como sucede en la geografía, y otras variables están latentes y en ocasiones son dimensionales (por ejemplo, la profundidad). Así como el agua se encuentra con mayor frecuencia en el fondo de los barrancos, las sombras de una cara aparecen con más frecuencia en los huecos de la cara que en la punta de la nariz.
Por lo tanto, nuestro trabajo en las dimensiones 2D y 3D empieza con el trabajo sobre la imagen y seguidamente pasaremos a otros aspectos de la espacialidad. Recuerde también que existe un continuo de pensamiento entre las dimensiones 1D/2D de series de tiempo y las dimensiones 2D/3D de la imagen, la geografía, la propagación de sonidos u ondas. Tanto es así que las técnicas de modelado, optimización o predicción adquiridas en uno de estos campos de investigación son útiles en el resto (con algunos cambios de vocabulario y limitaciones o restricciones).
1. Creación, visualización, lectura y escritura de imágenes
Una imagen en blanco y negro se puede almacenar como una matriz de píxeles (alto y ancho de la imagen). Cada píxel tiene una intensidad más o menos fuerte (su intensidad de gris), normalmente codificada con un valor que va desde 0 hasta 255 (incluido) en el caso de las imágenes que se utilizan en los ejemplos que encontrará sobre el procesamiento...
Como crear una muestra: LHS (hypercube latin)
Para crear un muestreo eficiente, especialmente cuando el problema tiene muchas dimensiones, es tentador construir un muestreo donde haya un mínimo de interacciones entre las variables. Obviamente, este tipo de muestreo es más útil cuando se sospecha una covarianza débil entre ellas porque este método de muestreo no ayudará a capturar fácilmente el efecto de las interacciones entre variables.
En el caso de problemas que se presentan en dimensiones pequeñas (2D, 3D) pero con muchos puntos por paquete de observaciones (imagen, geografía, etc.), estos métodos de muestreo también tienen todo su significado.
Los jugadores de ajedrez conocen el problema de las ocho reinas en un tablero de ajedrez, que consiste en poner ocho reinas en el tablero de ajedrez que no puedan atacarse. Los cuadrados mágicos, los sudokus y las ocho reinas son problemas para construir una distribución de objetos bajo restricciones de interacción precisas y, a menudo, mínimas.
LHS (Latin Hypercube Sampling) parece un problema de «torres» de ajedrez, cada torre no debe poder atacar a las demás.
La idea es simple: segmentamos cada variable, y solo permitimos una observación por cada intersección (sección del hipercubo general) compuesta por un borde y que se corresponde con un segmento de una dimensión. La observación...
Trabajar sobre datos en el espacio
1. Variograma
a. Campo y variable regionalizada
Durante el programa «meteorológico» de la televisión, el profesional hace su presentación sobre un mapa en el que se detallan las temperaturas: utiliza un campo escalar (scalar field).
En cada ubicación, definida por sus coordenadas 2D en el mapa, hay una temperatura (un valor escalar). En el mapa meteorológico, solo ciertos puntos están marcados con una temperatura; es un muestreo: podríamos haber elegido estos puntos usando LHS, pero probablemente preferimos recopilar las temperaturas en los puntos que corresponden a las diferentes grandes ciudades.
Para deducir la temperatura en su casa si no vive en una gran ciudad, es necesario interpolar (realizando un suavizado). Tiene una infinidad de estrategias más o menos efectivas: un suavizado brusco usando las dos ciudades más cercanas y tomando un promedio, el mismo suavizado tomando un promedio ponderado por la inversa de las distancias, el uso de tres ciudades que forman un triángulo a su alrededor y calcular los pesos como el inverso de los coeficientes baricéntricos de su ubicación, visto como el baricentro de las tres ciudades, etc.
Cuando el presentador del tiempo comenta la situación del viento en el mapa, indica su velocidad y dirección: por lo tanto, ha definido vectores de «viento» en varios lugares del mapa. Algunas veces, pequeñas flechas de diferente longitud representan estas velocidades en cualquier punto del mapa. Estamos hablando de un campo vectorial (vector field).
Un piloto de globo aerostático seguramente no estaría satisfecho con los campos 2D del mapa; sin duda querría saber la fuerza de los vientos y su dirección en tres dimensiones, por ejemplo: el viento a 100 m de altitud en tales coordenadas GPS es ascendente y Nor-Noroeste, 60 km/h.
La diferencia entre los valores de un campo escalar entre dos puntos, puede generar un campo vectorial inducido. Si este campo vectorial es «proporcional» a la variación del campo escalar en todas sus dimensiones, hablamos de gradiente: como en el caso de nuestro niño que busca sus huevos de Pascua y que intenta orientar su velocidad de movimiento en la dirección en la que se «quema» cada vez más.
En geografía, meteorología, prospección...
Conocimientos prácticos útiles
1. Trazar una curva ROC
Ya hemos introducido la curva ROC y la noción de AUC en el primer capítulo. El concepto no es muy complicado, pero algunas veces resulta difícil dibujar estas curvas al inicio. Se trata de curvas que sus compañeros esperan, por lo que aquí hay un código «hiperclásico» para generar una.
Para construir nuestro conjunto de datos, usamos el código LHS que hemos visto más arriba, pero con 300 observaciones en lugar de 100.
Nuestro ejemplo usa árboles de decisión. Hicimos una función perturbada para generar clases binarias. Esta parte del código no es ninguna sorpresa.
require(caret)
require(party)
set.seed(1)
y <- 10*df[,1] + # una función extraña
7* df[,2] * rnorm(nrow(df))+
3*sin(df[,3])+
2*sin(df[,4])*runif(nrow(df))
y <- ifelse(y < 7,0,1) # fabricación de clases
sum(y)/length(y) # % clases
y <- factor(y) # creación de factors
df_<- data.frame(df,y) # más sencillo para:
p <- createDataPartition(y=df_$y,
p= 50/100,
list=FALSE)
training <- df_[p,]
test <-...Gradiente Boosting y Generalized Boosted Regression
1. Los grandes principios
Los principios del boosting y de los métodos de gradiente ya se han presentado en los capítulos anteriores (desde el primer capítulo). Ahora nos centraremos en una implementación práctica, particularmente fácil de manejar para conjuntos de datasets de tamaño razonable, como los que encontrará en las competencias de data scientist: la Generalized Boosted Regression.
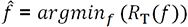 .
.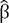 estimados de la función, como
estimados de la función, como 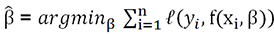 .
.En el caso no paramétrico, permanecemos en la primera formulación en función del riesgo, y el método del gradiente se aplica directamente al riesgo.
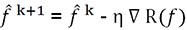 .
.Pero en el caso paramétrico, es posible aplicar el método de gradiente directamente a los parámetros, y esto es precisamente lo que hay que hacer.
Todo esto plantea algunos problemas prácticos. De hecho, el modelo tiende a superponerse en todas las observaciones (en lugar de crear una función resultante que pueda generalizarse). Los casos para los que diferentes observaciones con los mismos valores explicativos conducen a una respuesta diferente, pueden desestabilizar el descenso del gradiente (no en vano hemos desarrollado otros métodos de optimización, como los que vimos anteriormente).
Una conclusión práctica (cf. el trabajo de Friedman) es basar el descenso del gradiente en funciones poco sensibles al valor de un punto (y, por tanto, sobre todo, no depender directamente...
 Ediciones ENI Editorial | líder en informática
Ediciones ENI Editorial | líder en informática


