Análisis numérico y matemáticas operativas

1. Consideraciones prácticas

En este capítulo, abordaremos los cálculos numéricos y las expresiones matemáticas que los ingenieros utilizan más habitualmente o que son más comunes en machine learning. No se trata de un curso de análisis numérico, de matemáticas o matemáticas específicas para machine learning. Gran parte del conocimiento se presenta con un enfoque sintáctico y, cuando las explicaciones son más detalladas, se intentan evitar decepciones durante el uso práctico de las herramientas de cálculo que están a su disposición.

Atención: a menos que se indique lo contrario, consideramos que nos encontrarnos en una base ortonormal de un espacio vectorial euclidiano (por lo tanto, de dimensión finita sobre el campo de los números reales y provisto de un producto escalar), y que tenemos una presentación en esta base de datos de los objetos que usaremos (o en el sistema de coordenadas cartesianas asociadas si tiene sentido).

Recordemos algunas características de cálculo, relacionadas con este estado de cosas (estos aspectos ya se han mencionado de otra manera con anterioridad en el libro).

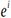En la base B formada por vectores , si nuestro espacio vectorial está dotado del producto escalar 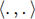, un vector cualquiera del espacio se puede escribir de la siguiente manera: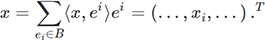

El signo T, que significa transpuesto, no es útil para la definición, pero está presente para recordar que tradicionalmente adoptamos una representación de vectores en «columnas» (una columna es muy engorrosa visualmente, por lo que escribimos una fila y la transponemos).

Normalmente es suficiente con diseñar el producto escalar en cuestión con un «.». De ahí la expresión «dot» para hacer referencia a él.

La norma más utilizada es la euclidiana .

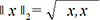Cuando no hay ambigüedad, es inútil suponer el índice 2 en la parte inferior derecha de las dobles barras.

Recuerde que, para construir un vector de fila en el espacio R, es suficiente con usar la función c(...). Ilustramos este cálculo de norma euclidiana:

x <- c(1,20,30)         # un vector de fila x (vector) 
sqrt(sum(x * x))        #...

1. Ejemplo de creación de una base ortonormal

Aquí proponemos crear una base ortonormal a partir de una familia de vectores y después comprobar esta propiedad. La base construida estará «más cerca» de la familia original. Llamamos su atención sobre el hecho de que la familia en cuestión genera un subespacio vectorial, pero no es explícitamente una base.

Por el contrario, para simplificar el ejemplo de R, consideramos una familia de vectores que ya forman una base del espacio vectorial completo considerado. Podríamos haber tratado una familia que genera un subespacio de dimensión inferior y obtener una base ortonormal de este subespacio. De hecho, esta es una de las aplicaciones más naturales de la función orth que vamos a utilizar.

Si no está familiarizado con estas técnicas, observe atentamente las manipulaciones de vectores columna. Están escritos de una manera mucho menos compacta que en los ejemplos que puede encontrar en otros lugares, pero le permitirán evitar muchos errores prácticos durante sus manipulaciones.

# familia de vectores, no ortonormales 
v1 <- matrix(c(1, 
              1, 
              0), ncol = 1) 
 
v2 <- matrix(c(0, 
              2, 
              0), ncol = 1) 
 
v3 <- matrix(c(0, 
              0, 
              3), ncol = 1) 
 
M <- cbind(v1,v2,v3)          # matriz...

1. Función de una variable

a. Exploración de varias trazas

Tenemos muchos métodos para trazar funciones. Analicemos los más sencillos. El ejercicio básico es trazar dos funciones en el mismo gráfico. Aquí las funciones son sencillas y naturalmente vectorizadas; no olvide vectorizarlas si es necesario.

# definición de las dos funciones 
f <- function(x){exp(-x)*sin(x)} 
g <- function(x){exp(x)*sin(x)+1000} 

Con R-base, la sintaxis es muy sencilla.

curve(f,-10,10, col = "red", ylab = "f y g") 
curve(g,-10,10, col = "blue", add = TRUE) 
grid()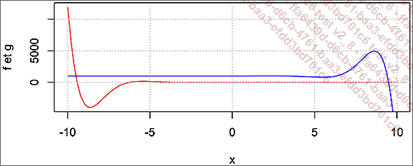 

Dos funciones

Vamos a introducir un método que ya hemos utilizado al inicio del libro, que consiste en discretizar las variables antes de emplearlas en un gráfico. Esta será la forma de proceder cuando usamos pracma; aquí, a través de su función plotyy, que tiene como objetivo trazar dos curvas, pero con escalas, si es necesario, diferentes en la ordenada, lo que puede ser muy útil si lo que queremos es comparar el aspecto de dos funciones y, sobre todo, mostrar su posible sincronización o desincronización en el eje x.

x_  <- linspace(-10,10,100 + 1) # discretización de x vía  
pracma::linspace 
                                # -10 -9.8 ... 0 ... 9.8 10 
 
plotyy(x_, f(x_),               # f y g no tienen la misma escala 
      x_, g(x_))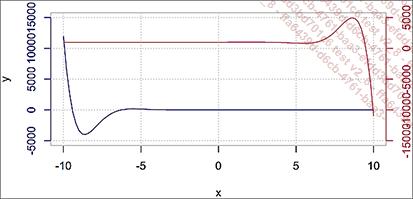 

Dos funciones, pero con dos escalas

Por supuesto, podría usar ggplot2 para crear este tipo de gráfico, pero no entraremos en los detalles de las opciones porque ya se discutieron anteriormente en el libro.

A continuación se muestra otra posible representación, por facetas, esta vez en ggplot2: 

f <- function(x){exp(-x)*sin(x)} # definir su función 
x_  <- linspace(-10,10,100 + 1)  # discretización de x vía pracma::linspace 
                                 # -10 -9.8 ... 0 ... 9.8 10 
p1 <- ggplot(data.frame(x = x_), aes(x = x)) # observe el uso de data.frame 
p1 <- p1  +...

1. Derivada simbólica y numérica con R-base

Como ya sabemos, es fácil calcular una derivada simbólica sencilla con las funciones básicas de R.

e <- expression(x^2+3*cos(x)- 1/x) 
d <- D(e,'x') 
d 
 
##> 2 * x - 3 * sin(x) + 1/x^2 

Podríamos evaluarlo por medio de efectos secundarios de la siguiente manera, pero no es muy «limpio».

x <- pi 
eval(d) 
 
##> [1] 6.384506 

Es más genérico construir una función verdadera insertando en su cuerpo la expresión obtenida mediante la evaluación de la expresión resultante de la derivación simbólica....

1. Cálculo de una integral múltiple

Para continuar con esta demostración de que R es un biotopo ideal para los cálculos científicos, consideremos la integral triple de una función f en un dominio D sobre un elemento de volumen dV.

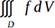
En tal caso, f a menudo se asemeja a una densidad. Si f es la función unidad, simplemente obtenemos el volumen del dominio D.

Considerando que f es una función de tres variables, tenemos .

Lo que se expresa en detalle de la siguiente manera .

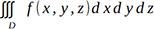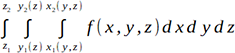Para que pueda recordarlo, observe que la integral más anidada (sobre dx) es una función de y y z y que la integral sobre dxdy es una función de z.

Ahora vamos a usar la función que permite calcular una integral como esta con el paquete pracma. Observe cómo se expresan los límites del dominio que hemos elegido como ejemplo.

f <- function(x,y,z) x + y + 10*z    # la función a integrar 
 
                                     # definición del dominio D 
z1 <- 0 
z2 <- 1 
 
y1 <- function(z) z 
y1 <- Vectorize(y1)     # vectoriza y1, inútil en este caso porque y1 es muy 
                        # sencillo (hecho aquí para llamar...

1. Otras funciones especiales

No vamos a dar un curso, ni siquiera una introducción matemática a la noción de función especial, sino únicamente llamar su atención sobre dos aspectos:

Estas funciones especiales no se mencionan aquí porque representen curiosidades matemáticas, sino por su utilidad en muchos cálculos prácticos. La idea es que no se bloquee cuando quiera implementar un cálculo, utilizando las que se encuentre durante su lectura de artículos de investigación.

a. Funciones de Airy y de Bessel

Las dos funciones de Airy son las soluciones de una ecuación diferencial difícil, que tiene su utilidad en varias áreas, incluyendo la mecánica cuántica (caso de la ecuación de Schrödinger independiente del tiempo), la mecánica de continuos (cálculo del tensor de las restricciones de los cálculos de elasticidad en un caso plano), la difracción de ondas, etc. Nos pareció útil exponer desde otro paquete estas funciones especiales que encontramos en estas funciones especiales que encontramos en Matlab y que no están disponibles en pracma.

La ecuación diferencial (con soluciones en los números complejos) parece sencilla, pero resulta difícil de resolver.

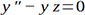
Las funciones Airy del paquete Bessel calculan estas funciones y sus derivadas...

1. Funciones reales de un real

Antes de entrar en el corazón del tema del cálculo diferencial, volveremos a ver las funciones que nos permiten calcular una derivada e introducir un poco de robustez en nuestros cálculos de derivadas con pracma.

Consideramos aquí una función real de un real.

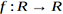
f <- Vectorize(function(x){exp(-x)*sin(x)+ x^3}) 

Hay muchas formas de obtener su primera derivada. Uno de los métodos que proporciona la mejor precisión resulta ser el de «complex step», que no es muy sensible al ruido relacionado con numerosas iteraciones y que, por lo tanto, se puede usar en algoritmos muy iterativos.

complexstep(f,1)          # derivada robusta 
 
##> [1] 2.889206 

Tener los resultados de funciones derivadas vectorizadas nos permite aplicarlos miembro a miembro a los componentes de cualquier vector.

complexstep(f,c(1,2,3))   # derivada de cada componente del vector 
 
##> [1]  2.889206 11.820621 26.943685 

También puede usar la función fderiv, que le permite desplazarse hacia la izquierda o la derecha del punto considerado, lo que puede ser muy útil cuando la función no es diferenciable precisamente en el punto considerado. Además, la función fderiv permite calcular derivadas de orden superior.

La siguiente función no es derivable en x = 2: .

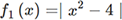f1 <- function(x) abs(x^2-4) 
curve(f1, -4, +4); grid()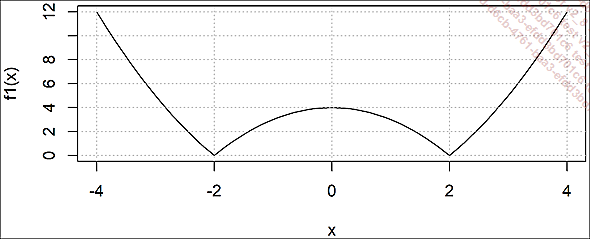 

Curva no derivable en todos puntos

Sin embargo, si intenta derivarla en este punto, obtendrá un resultado (falso):

fderiv(f1,2)       # resultado engañoso 
 
##> [1] 6.055514e-06 

De hecho, había que calcular la derivada por la izquierda y por la derecha:

fderiv(f1, 2, method = "backward") # por la izquierda 
 
##> [1] -4 
 
fderiv(f1, 2, method = "forward")  # por la derecha 
 
##> [1] 4 

El paquete mosaicCalc nos permite crear fácilmente una función siendo la derivada de otra función...