Desarrollo a partir de algoritmos
Presentación de la noción de algoritmo
Un algoritmo es la descripción de las operaciones necesarias para obtener un resultado a partir de valores de entrada: los "datos". Un programa es un algoritmo escrito en un lenguaje concreto. Volveremos sobre esto más adelante.
Una receta de cocina se puede considerar un algoritmo. Para que sirva de ejemplo, la fabricación de un pastel se basa en ingredientes (leche, mantequilla, harina, azúcar...) y se aplicará un procedimiento metódico (receta de la abuela) para utilizar estos ingredientes (mezcla, tiempo de cocción...). Habrá comprobado en su día a día que utilizamos algoritmos sin darnos cuenta realmente (recetas, noticias, planos de diseño, plantillas...).
Volvamos sobre nuestro ejemplo de la receta de cocina. En su ausencia, es posible conseguir el plato con una sucesión de intentos (ensayos, tiempo de cocción aproximado). Evidentemente, esta forma de proceder (aunque para algunos sea satisfactoria) no es eficaz (se pierde tiempo y es un lío de ingredientes).
La programación va a ser el medio de definir y especificar al ordenador el conjunto de operaciones necesarias para resolver un problema. Se trata de la traducción a un lenguaje comprensible por la máquina de las secuencias de acciones que se deben aplicar a los datos, en el marco de un procesamiento informático. Aquí también...
Noción de variable
1. Presentación de las nociones de variable y tipo
Un algoritmo manipula objetos sobre los que puede realizar acciones. Los objetos simples son:
-
números (3.14159, 1980, 9...),
-
caracteres ("A", "9"...) y cadenas de caracteres ("PAULINA"...),
-
valores booleanos o lógicos (verdadero o falso).
Para poder manipular estos objetos, hay operaciones disponibles. Estos objetos, así como las operaciones asociadas, se deben definir perfectamente. Analicemos los tres ejemplos siguientes, que son situaciones de intercambio entre un cliente y un vendedor.
Ejemplo 1:
-
"Buenos días, quisiera 1 kg y 1 kg."
-
"??"
Ejemplo 2:
-
"Buenos días, señor, quisiera 1 kg de arroz y 1 kg de vino."
-
"Aquí está su kilo de arroz y ¿qué más quería?"
Ejemplo 3:
-
"Buenos días, señor, quisiera 1 kg de arroz y 1 litro de vino."
-
"Le he puesto todo en esta bolsa."
En estos ejemplos, comprobamos la necesidad de:
-
citar la naturaleza de los objetos que vamos a manipular (arroz, vino...),
-
no utilizar estos objetos de cualquier manera (el arroz se pesa, el vino se bebe...) es decir, para cada naturaleza de objeto, hay operaciones particulares.
Se llama tipo a la asociación:
-
de una naturaleza de objeto (arroz, vino, o incluso enteros, reales...),
-
y las operaciones asociadas (pesar, lavar, cocinar el arroz, sumar, multiplicar enteros...).
2. Tipos básicos y operaciones asociadas
Hay cuatro tipos básicos: entero, real, booleano y carácter.
El tipo entero:
-
Los valores son números enteros.
-
Notación: se utiliza la notación decimal (ejemplos: 365, -15).
-
Operaciones: suma, resta, multiplicación, división entera, módulo (resto de la división entera), etc.
El tipo real:
-
Los valores son números reales.
-
Notación: el punto anglosajón se sustituye por la coma (ej.: 124.89, 0.136, 1986).
-
Operaciones: las que se usan habitualmente con los números reales en aritmética.
El tipo booleano:
-
Solo hay dos valores booleanos: verdadero o falso.
-
Notación: Verdadero y Falso.
-
Operaciones: se utilizan los operadores lógicos usuales (No, O e Y).
Recordemos el funcionamiento de los operadores lógicos No, Y y O, con esta tabla resumen:
|
A |
No A |
|
Verdadero |
Falso |
|
Falso |
Verdadero |
|
A |
B |
A O B |
|
Verdadero... |
Manipulación de las variables
1. Nomenclatura de las variables
Durante el análisis de un problema, a menudo tenemos que descomponer este en subproblemas, que se deben resolver en un orden secuencial concreto. Cada subproblema genera resultados que se pueden utilizar en los subproblemas que siguen. Por tanto, para poder manipular estos resultados, conviene asignarles un nombre. Esta nomenclatura se hace a través de un identificador. También se habla muy a menudo de variable en memoria.
A cada variable en memoria, se le asocian las siguientes características:
-
su denominación, que se debe hacer con sentido (dos resultados diferentes se designan por identificadores diferentes),
-
su tipo (conjunto al que pertenece el valor que designa).
Estas características se precisan durante la declaración de la variable en memoria.
Sintaxis de la declaración:
|
Tipo IDENTIFICADOR |
Tipo es el tipo e IDENTIFICADOR es la denominación de la variable en memoria.
Ejemplos:
|
Real PI Car SEPARADOR Bool TEST Ent NBMESES, NBDIAS |
Una vez que se define una variable en memoria, no se puede cambiar su tipo.
Cualquier variable en memoria utilizada en un algoritmo se debe haber declarado con antelación.
En lo sucesivo, se ha elegido nombrar a las variables en memoria en mayúsculas, para mejorar su legibilidad. Debe saber que hay muchos lenguajes de programación que son sensibles a la diferencia entre mayúsculas y minúsculas de las variables en memoria (una variable CANTIDAD es diferente de una variable Cantidad).
Evidentemente, en programación (JavaScript en nuestro caso), se pueden proponer diferentes convenciones de nomenclatura.
En JavaScript, para las variables en memoria (y las funciones), la convención comúnmente aceptada es "camelCaps", es decir, que los nombres deben empezar sistemáticamente por una minúscula y después se insertan mayúsculas al inicio de cada palabra que aparece en el nombre de la variable. Por ejemplo, una variable como ACUMULADO_ANUAL (la convención en esta presentación de la algoritmia) se codificará como acumuladoAnual en JavaScript.
Puede observar que, en este libro, muchos scripts JavaScript no usan la convención camelCaps. Se ha decidido no modificar los nombres de las variables en memoria de los algoritmos subyacentes.
2. Asignación
La asignación...
Funciones predefinidas
Una función predefinida es un "microprograma" autónomo, al que es posible pedir un procesamiento (un cálculo en general), pasando uno o varios argumentos. Una vez que el cálculo está asegurado, la función restituye un valor de retorno (la respuesta) al solicitante (secuencia de código que llama a la función). Esta noción seguramente le es familiar si, por ejemplo, ha utilizado funciones nativas en Microsoft Excel (SUMA, BUSCAR...).
Veremos más tarde en esta presentación de la algoritmia (y también, sobre todo, en JavaScript) cómo desarrollar sus propias funciones.
El objetivo aquí no es enumerar la lista de funciones habituales en algoritmia (además pueden variar de un autor a otro), sino mostrarle cómo se pueden usar. Se utilizará una presentación a través de ejemplos o ejercicios.
1. Ejercicio n.°4: Visualización de la longitud de un nombre
Enunciado
Escribir un algoritmo que permita introducir con el teclado un nombre para mostrar el número de caracteres
Complemento del ejercicio: Una función Longitud(variable_cadena) predefinida se utilizará para determinar el número de caracteres de la palabra.
Correcciones
|
Inicio |
|
|
Co Declaraciones Fco Car NOMBRE |
|
|
Co Introducción del nombre por el teclado Fco Escribir("Nombre:") NOMBRE <- Leer |
|
|
Co Visualización del resultado Fco Escribir(NOMBRE, " contiene " , Longitud(NOMBRE), " carácter(es)") |
|
|
Fin |
|
E incluso:
|
Inicio |
|
|
Co Declaraciones Fco Car NOMBRE Ent NB_CAR |
|
|
Co Introducción del nombre por el teclado Fco Escribir("Nombre: ") NOMBRE <- Leer |
|
|
Co Visualización del resultado Fco NB_CAR <- Longitud(NOMBRE) Escribir(NOMBRE, " contiene " , NB_CAR, " carácter(es)") |
|
|
Fin |
|
2. Ejercicio n.°5: Determinación de iniciales...
Procesamientos condicionados
En muchas situaciones, las acciones solo se realizan si se cumplen determinadas condiciones:
-
Una ecuación de segundo grado tiene 0, 1 o 2 soluciones reales, según sea el discriminante negativo, nulo o positivo.
-
Si una cantidad de artículos en stock baja de un determinado umbral, hay que hacer un pedido.
-
Si hace bueno, entonces vamos a la playa. En caso contrario, hacemos algoritmia juntos.
-
Si no hace bueno, entonces hacemos algoritmia juntos.
Cada una de estas opciones está condicionada por una expresión booleana que, mientras sea verdadera, implica la ejecución del procesamiento asociado.
La sintaxis de la algoritmia para programar los procesamientos condicionados es sencilla:
|
Si Condición |
|
|
Entonces |
|
|
T1 |
|
|
[En caso contrario |
|
|
T2] |
|
|
Finsi |
|
Algunas observaciones sobre esta estructura tan intuitiva:
-
Condición es una expresión con resultado booleano (Verdadero o Falso).
-
T1 y T2 son los procesamientos.
-
Finsi significa el fin del si.
-
Existe una forma simplificada, sin alternativa (sin En caso contrario T2).
-
Comprobar la condición se hace en una hipótesis de condición verdadera.
-
Dibujar un trazo vertical (a la izquierda) entre Si y Finsi será un medio mnemotécnico para no olvidar el Finsi.
-
Piense en indentar los procesamientos T1 y T2.
El organigrama de flujo correspondiente a esta estructura es el siguiente:
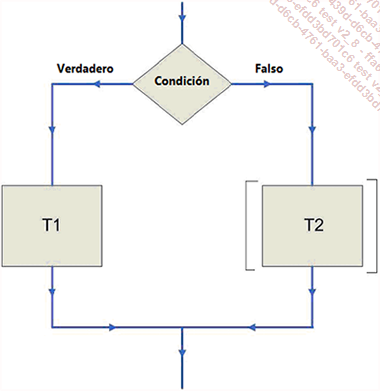
En el ejemplo que se presenta a continuación, a una variable NBLU se le asigna un valor numérico introducido con el teclado y el algoritmo indica si se trata de un valor par o impar:
|
Inicio |
||
|
Co Declaraciones Fco Ent NBLU |
||
|
Co Introducción con el teclado Fco Escribir("Número: ") |
||
|
NBLU <- Leer |
||
|
Co Determinación de la parte Fco Si NBLU Mod2 = 0 |
||
|
Entonces |
||
|
Escribir(NBLU, " es par") |
||
|
En caso contrario |
||
|
Escribir(NBLU, " es impar") |
||
|
Finsi |
||
|
Fin |
||
1. Ejercicio n.°6: Polinomio de segundo grado
Enunciado
Calcular las raíces de un polinomio de segundo grado Ax2+Bx+C (con A<>0 aunque esta prueba no se hará aquí). Los valores A, B y C se introducirán con el teclado.
Corrección
|
Inicio |
|||
|
Co Declaraciones Fco Real A, B, C, DELTA |
|||
|
Co Introducción de los argumentos Fco Escribir("A: ") A <- Leer |
|||
|
Escribir("B: ") B <- Leer |
|||
|
Escribir("C: ") C <- Leer |
|||
|
Co Cálculo del discriminante Fco DELTA <-... |
Estructuras iterativas
1. Concepto de iteraciones
En la mayor parte de los problemas, determinadas acciones se deben ejecutar varias veces.
Cuando el número de repeticiones es grande, resulta pesado rescribir n veces la misma secuencia de código. Esta rescritura es imposible cuando el número de repeticiones (iteraciones) es desconocido a priori (trazar un conjunto de datos hasta que no haya más).
Es necesario poder expresar la repetición de una acción que, una vez inicializada, continuará hasta que se produzca un determinado evento. Este evento de parada se especificará en el algoritmo con una condición.
2. Estructuras iterativas básicas
Vamos a estudiar cuatro tipos de iteraciones (bucles), que tendrán su equivalente en los principales lenguajes de programación.
Bucle "Mientras" con una comprobación inicial de iteración:
|
Mientras Condición Hacer |
|
|
Acciones |
|
|
Volverhacer |
|
Bucle "Hasta que" con una comprobación inicial de iteración:
|
Hastaque Condición Hacer |
|
|
Acciones |
|
|
Volverhacer |
|
Bucle "Mientras" con una comprobación final de iteración:
|
Hacer |
|
|
Acciones |
|
|
Mientras Condición Volverhacer |
|
Bucle "Hasta que" con una comprobación final de iteración:
|
Hacer |
|
|
Acciones |
|
|
Hastaque Condición Volverhacer |
|
Estos cuatro bucles tienen un determinado número de puntos en común:
-
Hastaque es una abreviación para Hasta que
-
Mientras es una abreviación para Mientras
-
Condición, es una expresión booleana de resultado Verdadero o Falso
-
Acciones representa una secuencia de acciones
Con las dos últimas iteraciones para las que se hace la comprobación del final de bucle, las Acciones se realizan al menos una vez.
Los bucles "Mientras" y "Hasta que" tienen un funcionamiento muy parecido, en la medida en que es suficiente con invertir la condición para pasar de una sintaxis a otra. Por ejemplo, CONTADOR > 10 en el caso de un bucle "Mientras" se convertirá en CONTADOR <= 10 en caso de un bucle "Hasta que".
El siguiente diagrama de flujo corresponde a las estructuras "Mientras" y "Hasta que" (con una comprobación inicial de iteración):
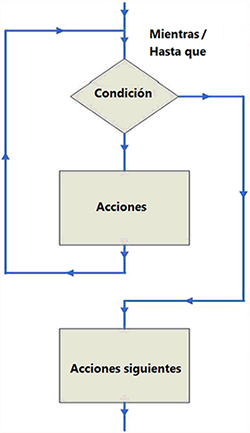
En caso de un bucle Hastaque:
-
la flecha que une "Condición" a "Acciones" corresponde...
Tabla de dimensión única
Una tabla agrupa varios valores del mismo tipo. Globalmente, podemos nombrar todos los valores o designar de manera precisa uno de ellos con una operación de scripting.
Por ejemplo, consideremos ALFABETO al conjunto de letras del alfabeto. En este caso:
-
ALFABETO designa una tabla que podrá servir para almacenar el conjunto de letras del alfabeto.
-
ALFABETO(14) podría representar la letra "N".
-
El entero 14 se llama índice.
En un algoritmo, como sucede con las variables (simples) vistas hasta ahora, las tablas se deben declarar antes de poder utilizarlas. La sintaxis de declaración es:
|
Tipo IDENTIFICADOR(INF: SUP) |
Observe que a nivel de esta declaración:
-
IDENTIFICADOR es el nombre global de la tabla (nombre libremente elegido por el programador, en mayúsculas si es posible).
-
Tipo indica el tipo de los elementos de la tabla, y todos los elementos de la tabla tienen el mismo tipo (Entero, Real, Bool, Carácter).
-
INF y SUP son, respectivamente, los extremos inferior y superior del intervalo de variación del índice de la tabla. Una tabla como esta tiene N elementos, donde N = SUP - INF + 1.
-
INF y SUP son constantes definidas con antelación (sin dimensionamiento "dinámico", aunque determinados lenguajes de programación lo permiten).
-
En determinados lenguajes de programación, el valor INF no se puede expresar. En este caso, el valor...
Tabla con dimensiones múltiples
Cuando los elementos de una tabla son ellos mismos tablas, se habla de tabla de varias dimensiones.
A nivel de la declaración de este tipo de tabla, hay que declarar los límites del índice para cada una de las dimensiones, lo que no es ya una sorpresa:
Tipo IDENTIFICADOR(INF1: SUP1, ..., INFi: SUPi, ..., INFn: SUPn)
Para acceder a las diferentes celdas de una tabla de varias dimensiones, hay que indicar un valor de índice para cada una de ellas. A modo de ejemplo, para una tabla de dos dimensiones (tabla de líneas divididas en columnas como una matriz 2D en Microsoft Excel), el primer índice normalmente designa el número de la línea y el segundo, el número de la columna de la celda a la que se hace referencia. Por tanto, la sintaxis es:
IDENTIFICADOR(ÍNDICE1, ..., ÍNDICEi, ..., ÍNDICEn)
1. Ejercicio n.°15: Minihoja de cálculo
Enunciado
A partir de la tabla TB de dos dimensiones con cuatro líneas y cinco columnas, realizar los siguientes procesamientos:
-
Introducir con el teclado valores en las tres primeras líneas y las cuatro primeras columnas (se conserva la última línea y la última columna libres, para los totalizadores de líneas y columnas).
-
Añadir las columnas de última línea y las líneas en última columna.
Corrección
|
Inicio |
|||
|
Co Declaraciones de las variables... | |||
Procedimientos, funciones y paso de argumentos
1. Los objetivos
Estos nuevos mecanismos permiten al programador tratar un problema sin preocuparse, inicialmente, de las reglas detalladas de los subproblemas. Se trata de herramientas muy similares a las funciones matemáticas.
En programación, un procedimiento o una función, representa un algoritmo que opera con argumentos o argumentos formales (valores ficticios de alguna manera). La ejecución de este algoritmo se genera con la llamada del procedimiento o de la función. Los datos de este algoritmo llamado son los argumentos efectivos (que provienen del algoritmo que llama).
El interés metodológico de estos mecanismos en una primera etapa consiste principalmente en convertir los subproblemas en procedimientos (o en funciones) y tratar el problema general (o principal) como si estos subproblemas estuvieran solucionados. En una segunda etapa, se describen estos procedimientos o funciones. Otra ventaja es que, si el mismo subproblema se debe resolver varias veces con argumentos efectivos diferentes, el uso de un procedimiento o función permite una mejor legibilidad del algoritmo.
2. Los procedimientos
Comencemos el estudio de este mecanismo con la sintaxis de la declaración:
|
Procedimiento NOMBRE_PROCEDIMIENTO([Tipo1 IDFO1, ..., Tipoi IDFOi]) |
|
|
Cuerpo del procedimiento |
|
|
Fin_procedimiento |
|
En esta declaración:
-
NOMBRE_PROCEDIMIENTO es un nombre elegido libremente por el programador.
-
IDFOi es el nombre del enésimo argumento formal del procedimiento.
-
Tipoi es el tipo del enésimo argumento formal del procedimiento.
-
El procedimiento no devuelve valores a menos que intervenga sobre las variables (accesibilidad) globales.
-
Procedimiento y Fin_procedimiento son palabras reservadas.
La llamada de un procedimiento desde otro o desde el algoritmo principal se hace respetando el siguiente esquema:
|
NOMBRE_PROCEDIMIENTO(IDEF1, IDEFi, ..., IDEFn) |
con:
-
NOMBRE_PROCEDIMIENTO es un nombre elegido libremente por el programador,
-
IDEFi es el nombre del enésimo argumento efectivo.
3. Ejercicio n.°16: Llamada de un procedimiento con paso de argumentos
Enunciado
Llamar a un procedimiento que muestra el doble de los valores efectivos pasados como argumento (los dos valores pasados como argumento se introducen con el teclado).
Corrección
|
Inicio |
||
|
Co Uso de un procedimiento que muestra el doble de una pareja de valores Fco |
||
|
Co Procedimiento... | ||
 Ediciones ENI Editorial | líder en informática
Ediciones ENI Editorial | líder en informática