Algoritmos de regresión
La tarea de regresión
1. Definición
Junto con la clasificación, la tarea de regresión es una de las dos principales tareas de Machine Learning en el aprendizaje supervisado.
La regresión consiste en asociar un valor numérico (variable objetivo) a un conjunto de variables explicativas. A diferencia de la clasificación, en la que el valor predicho solo puede adoptar determinados valores (las categorías), en este caso se trata de una variable continua.
La mayoría de los algoritmos no tienen noción de los límites, y el valor previsto puede abarcar todos los valores posibles. Por lo tanto, a menudo es necesario un postprocesamiento para devolver el valor al rango posible (por ejemplo, entre 0 y 20 si se trata de una nota).
Atención: la regresión se utiliza para encontrar una correlación entre las variables explicativas y la variable objetivo. Esta correlación no debe confundirse con la causalidad. Por ejemplo, una correlación encontrada entre la capacidad de memoria y el número de dientes no significa que la pérdida de dientes sea la causa de la disminución de la memoria: puede haber otra razón no presente en los datos (como la edad).
2. Ejemplos de casos prácticos
La regresión se utiliza en muchos casos potenciales:
-
Predecir el precio de un producto o servicio en función de sus características, como el precio...
Entrenar y evaluar modelos
Antes incluso de ver cómo funcionan los principales algoritmos, es importante entender cómo se evaluarán los modelos, ya que la evaluación no depende del algoritmo.
La evaluación se llevará a cabo en el conjunto de validación cuando se elijan los hiperparámetros y/o el modelo, y en el conjunto de prueba al final del proceso, cuando se haya determinado el mejor modelo o modelos.
El conjunto de aprendizaje también se evalúa periódicamente. Aunque el objetivo de esta evaluación no es decidirse por un modelo, sino permitir comprobar si se ha producido el aprendizaje y si hay sobreajuste.
Con Scikit-learn, el proceso será siempre el mismo:
-
Crear un modelo especificando los parámetros deseados. En el caso de la regresión, la clase será Regressor (en el ejemplo, es un DecisionTreeRegressor, es decir, un árbol de decisión adaptado a la regresión).
-
Realizar el aprendizaje gracias fit, proporcionándole los datos de aprendizaje X e y.
-
Predecir los resultados en el dataset deseado utilizando predict (a partir de X datos, obtener los datos predichos).
-
Llamar a las distintas métricas deseadas (presentes en sklearn.metrics) usando como parámetros los resultados esperados y los datos predichos).
Las funciones y el proceso son los mismos que para la clasificación, con la diferencia de la preparación de los datos y el algoritmo utilizado. Del mismo modo, las métricas son diferentes porque dependen de la tarea en cuestión.
En términos de código, tiene el siguiente aspecto (usando el dataset de Boston):
import prepare
import sklearn.metrics
from sklearn.tree import DecisionTreeRegressor
# Cargando los datos
train_X, test_X, train_y, test_y = prepare.prepare_boston()
names = ['CRIM', 'ZN', 'INDUS', 'CHAS', 'NOX', 'RM', 'AGE', 'DIS',
'RAD', 'TAX', 'PTRATIO', 'B', 'LSTAT', 'MEDV']
# Crear un modelo
regressor = DecisionTreeRegressor(max_depth=5, random_state=42)
# Fit del modelo
regressor.fit(train_X, train_y)
# Predicciones
pred_y = regressor.predict(test_X) ...Usar algoritmos de clasificación
La mayoría de los algoritmos de clasificación pueden utilizarse para la regresión, con algunas adaptaciones.
1. Principio general
Los algoritmos de clasificación pueden predecir la clase (variable objetivo) a partir de variables explicativas. El número de clases se define de antemano.
En el caso de la regresión, existe un número infinito de valores posibles. Por tanto, los algoritmos de clasificación no pueden predecirlos todos.
Sin embargo, es posible determinar un número definido de valores potenciales. El algoritmo asociará a cada dato el valor de la variable objetivo potencial más próxima.
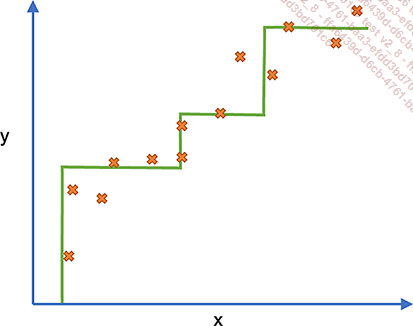
En el diagrama anterior, la predicción tiene forma de escalera. Cada meseta tiene una clase asociada.
Por supuesto, esto suele ser menos realista que un algoritmo de regresión específico, pero los algoritmos de clasificación son sencillos de aplicar, eficientes, no están sujetos a un sobreajuste y, en general, son fáciles de entender.
Sin embargo, existe una complejidad adicional en el caso de la regresión: el algoritmo también tendrá que determinar las diferentes etapas, además de clasificarlas (aunque esto generalmente implicará el muestreo de la amplitud deseada).
Dado que los algoritmos de clasificación se tratan en el capítulo Algoritmos de clasificación, su funcionamiento y parámetros principales no se revisarán en este capítulo.
2. Árboles de decisión y algoritmos derivados
a. Árboles de decisión
Los árboles de decisión pueden utilizarse para la regresión. En lugar de asociar una clase a cada hoja, se utiliza el valor medio de la variable objetivo para los elementos de esa hoja. Esto produce funciones «escalonadas».
Por lo tanto, el árbol se construirá de forma que limite la medición de una métrica de error, que puede elegirse (generalmente, se trata del error al cuadrado)....
Regresión lineal y variantes
1. Regresión lineal
La regresión lineal es el algoritmo fundador de la regresión. Consiste en determinar una línea recta en función de los distintos atributos.
En el caso particular de que solo haya un atributo, se trata de encontrar la línea recta con ecuación y=ax+b, donde a a se le denomina pendiente y a b ordenada al origen (punto donde la recta interseca al eje de las ordenadas o y).
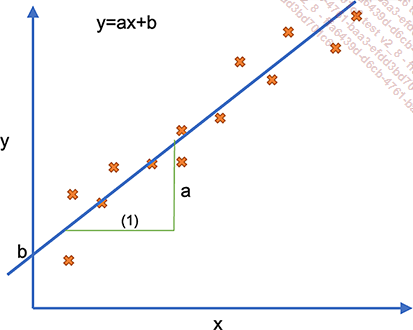
Como hay un número infinito de rectas, la recta devuelta es la que tiene el menor error cuadrático posible. La regresión lineal se denomina, por tanto, mínimos cuadrados ordinarios.
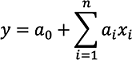 .
.La pendiente se sustituye por un conjunto de factores (ai) y la ordenada al origen por el primero de estos factores (a0).
Este algoritmo presenta una serie de ventajas: es sencillo y rápido de calcular, pero sobre todo es fácil de interpretar. Cada coeficiente indica la influencia de la variable en el resultado y, sobre todo, su significado, según sea positivo o negativo.
2. Aplicar en Scikit-learn
En Scikit-learn, la clase correspondiente a esta regresión lineal es LinearRegression. A continuación, se pueden solicitar los diferentes factores usando coef_ e intercept_.
La aplicación en el dataset de Boston es la siguiente:
from sklearn.linear_model import LinearRegression
from sklearn import metrics
regressor = LinearRegression()
regressor.fit(train_X, train_y)
pred_y = regressor.predict(test_X)
print(metrics.mean_squared_error(test_y, pred_y))
> 28.02570186948499
regressor.coef_
> array([ 2.31663318e-02, 1.66826494e-03, 2.56646848e-02,
3.16764647e+00, -1.54366811e+01, 4.90731544e+00,
-5.88145304e-03, -1.15437553e+00, 1.29222513e-01,
-8.90055909e-04, -9.09406332e-01, 1.26558793e-02,
-5.00701788e-01])
regressor.intercept_
> 22.723249676973637 La regresión lineal no es el algoritmo más potente, por lo que el resultado dista mucho de ser muy eficiente (aunque sea comparable a otros algoritmos).
La ordenada al origen...
Regresión polinómica
1. Principio
En muchos casos, la función utilizada para obtener la variable objetivo a partir de las variables explicativas no es lineal.
Todas las regresiones vistas anteriormente (mínimos cuadrados ordinarios, Ridge y Lasso) solo pueden resolver problemas lineales.
Existen otras formas de regresión, que no son lineales. La principal es la regresión polinómica, que permite hallar una función utilizando las dos variables explicativas y estas en un orden superior (x2, x3, x4...). El grado de la función es la potencia más alta.
También se pueden mezclar variables, por ejemplo, creando nuevas como multiplicaciones de las anteriores, como x1x2. Esta nueva variable es, por tanto, también de 2do orden.
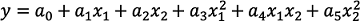 .
.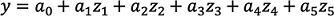 .
.Si las distintas características están precalculadas, la regresión polinómica es por tanto una regresión lineal en este nuevo espacio, y los algoritmos vistos anteriormente son perfectamente adecuados.
2. Regresión polinómica y Scikit-learn
No hay algoritmos de aprendizaje dedicados a la regresión polinómica en la biblioteca, solo los de regresión lineal (OLS, Ridge y Lasso, por ejemplo).
No obstante...
Caso especial de la predección
1. Predección y series temporales
El problema de predecir (Forecast)consiste en pronosticar la variable objetivo no a partir de variables explicativas, sino a partir de valores anteriores del objetivo.
En el caso del dataset de Boston, un problema de predicción podría consistir en pronosticar el precio medio de los pisos basándose en el historial de estos precios en lugar de en las características del inmueble.
Por lo general, no existe un dataset como tal, sino una serie de valores conocida como serie temporal.
Las series temporales suelen estar formadas por solo dos campos:
-
Fecha (opcional, se puede tratar de índices)
-
El valor en esa fecha
Por tanto, la variable objetivo es también la variable explicativa.
Una serie temporal puede considerarse como la descomposición de la serie en cuatro elementos:
-
La tendencia general, que puede ser estable, ascendente o descendente, lineal o no lineal.
-
Las estacionalidades, que son variaciones que se repiten con una frecuencia determinada, por ejemplo, un aumento de las ventas de adornos navideños cada año en noviembre/diciembre. Aunque el nombre sugiere estaciones, la frecuencia puede ser mucho más corta, por ejemplo, un cambio que depende de la hora del día.
-
Los ciclos, que son variaciones que se repiten con regularidad, pero sin una frecuencia definida. Por eso suele ser difícil predecir la próxima subida o bajada, como ocurre con la bolsa o, en menor medida, con el clima.
-
El ruido, que es una variación imprevisible que suele estar presente en los errores. Si el ruido es demasiado alto, no será posible hacer predicciones sobre las series temporales.
El siguiente gráfico muestra una serie temporal a lo largo de 100 pasos de tiempo, con valores comprendidos entre -10 y 60:
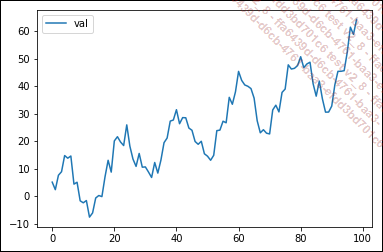
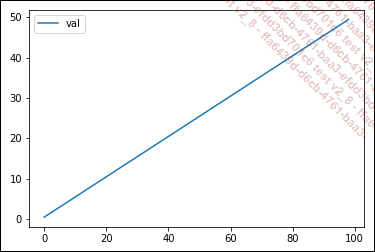
La tendencia general de esta curva es un crecimiento lineal con la ecuación y = x/2:
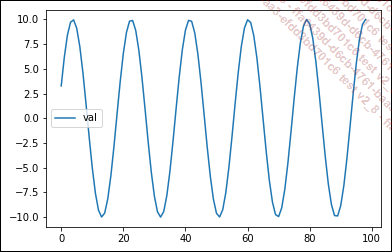
A esta tendencia general se añade una estacionalidad del periodo de algo menos de 20, con una amplitud de 20 (entre -10 y +10). La ecuación exacta de la curva es 10 * sen(x/3).
Además, existe un componente de ruido imprevisible, que sería el resto de la predicción. Por tanto, un modelo con una buena generalización tendrá un error igual a este (globalmente entre -4 y +4):
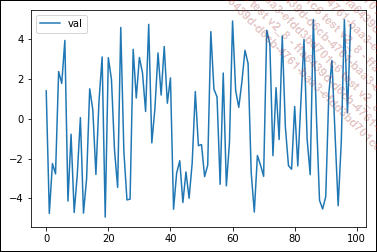
La curva anterior se ha obtenido utilizando el siguiente código:...
 Ediciones ENI Editorial | líder en informática
Ediciones ENI Editorial | líder en informática




