La tarea de clasificar

1. Definición

Junto con la regresión, la tarea de clasificación es una de las dos principales tareas de Machine Learning en el aprendizaje supervisado.

Se trata de asociar una etiqueta (label) a cada dato a partir de un conjunto de etiquetas (o categorías) posibles. En los casos más sencillos, solo hay dos categorías: se trata de una clasificación binaria o binomial. En los demás casos, se trata de una clasificación multiclase.

Las categorías deben determinarse antes de que se produzca cualquier forma de aprendizaje. Además, todos los datos utilizados para el aprendizaje deben tener ya una etiqueta, de modo que pueda conocerse la respuesta esperada: un aprendizaje supervisado.

En la gran mayoría de los casos, cada imagen estará asociada a una clase, pero hay algunos casos especiales, como:

Detección de objetos: el objetivo no es determinar la clase de una imagen en su conjunto, sino reconocer los distintos objetos presentes y sus posiciones respectivas.
Segmentación de imágenes: caso particular de la detección, consiste en indicar a qué clase pertenece cada píxel. Los píxeles de la misma clase se asocian generalmente al mismo color.

Estos casos especiales no se tratan en este capítulo.

2. Ejemplos de casos prácticos

Aunque el ejemplo más común en la literatura es determinar si una imagen...

Evaluar los modelos

Antes de ver cómo funcionan los principales algoritmos, es importante entender cómo se evaluarán los modelos. Esta evaluación no depende de los algoritmos elegidos.

La evaluación se llevará a cabo en el conjunto de validación cuando se elijan los hiperparámetros y/o el modelo, y en el conjunto test al final del proceso, cuando se haya determinado el mejor modelo o modelos.

El conjunto de aprendizaje también se evalúa periódicamente. Aunque el objetivo de esta evaluación no es decidirse por un modelo, permite comprobar si se ha producido el aprendizaje y si hay un sobreajuste.

Con Scikit-learn, el proceso será siempre el mismo:

Crear un modelo especificando los parámetros deseados. En el caso de la clasificación, la clase será un classifier (en el ejemplo, es un TreeClassifier, es decir, un árbol de decisión).
Realizar el entrenamiento utilizando fit, proporcionándole los datos de entrenamiento X e Y (es posible utilizar la validación cruzada o la optimización de hiperparámetros, como se ha visto en el capítulo anterior).
Predecir los resultados en el dataset deseado utilizando predict.
Llamar a las distintas métricas deseadas presentes en sklearn.metrics, con los resultados esperados y los datos predichos como parámetros.

En términos de código, se parece a esto (aquí en el dataset Iris):

import sklearn.metrics  
from sklearn.tree import DecisionTreeClassifier 
import prepare  
  
# Cargar datos (ver archivo prepare.py)  
train_X, test_X, train_y, test_y = prepare.prepare_iris() 
 
# Crear un modelo  
classifier = DecisionTreeClassifier(max_depth=2, random_state=42) 
  
# Fit del modelo  
classifier.fit(train_X, train_y) 
  
# Predicciones  
pred_y = classifier.predict(test_X) 
  
# Evaluar  
print(sklearn.metrics.confusion_matrix(test_y, pred_y))  
print(sklearn.metrics.accuracy_score(test_y, pred_y))

El resultado será el siguiente, correspondiente a las dos métricas solicitadas (matriz de confusión y accuracy (precisión)):

[[10  0  0]  
 [ 0  8  1]  
 [ 0  0 11]]  
0.9666666666666667

Para simplificar...

Árboles de decisión y algoritmos derivados

Los árboles de decisión se encuentran entre los algoritmos de Machine Learning más sencillos. Sin embargo, pueden ser muy potentes, especialmente cuando se utilizan junto con métodos de agrupación. De hecho, no es raro ver estos algoritmos en los primeros puestos de las clasificaciones de los retos Kaggle.

Kaggle es un sitio que presenta retos de Machine Learning, ideal para practicar, descubrir técnicas y aprender de los mejores en este campo.

1. Árboles de decisión

El árbol de decisión es, como su nombre indica, un árbol en sentido matemático, es decir, un conjunto de nodos unidos por ramas y que conducen a hojas.

En cada nodo, hay que realizar una prueba sobre el valor de una variable. Según el caso, es necesario entonces descender a uno de los nodos hijos. El proceso se repite hasta llegar a un nodo sin descendientes, que entonces se denomina hoja.

Indica la clase de datos procesados tras la clasificación.

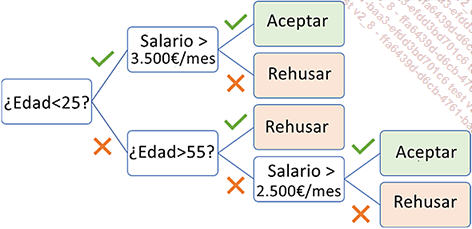
He aquí un ejemplo de árbol que podría utilizarse para indicar si se puede conceder o no un crédito a una persona. El árbol muestra que el primer criterio a tener en cuenta es la edad del solicitante. Si la persona tiene más de 25 años, debe seguirse la rama más baja.

Tomemos el registro de Alice (Edad = 34 años, Salario = 3000 euros/mes). El árbol indica que su crédito será aceptado porque:

no tiene menos de 25 años,
no tiene más de 55 años,
su salario es superior a 2.500 euros al mes.

No existe uno, sino varios algoritmos para obtener árboles de decisión. Varían en cuanto al resultado y a la forma de construir el árbol: ID3, C4.5, C5.0, CART, CHAID, etc. Sin embargo, sus principios fundamentales siguen siendo los mismos.

El algoritmo implementado en Scikit-learn es CART, que es una versión mejorada de C4.5. Nota: el algoritmo C5.0 está sujeto a una licencia de propiedad intelectual y, por lo tanto, no suele incluirse en el software.

a. Salir del árbol

Algunos algoritmos solo dan una clase (como el árbol anterior), mientras que otros dan probabilidades asociadas a cada hoja.

Para calcular las probabilidades de las hojas, el algoritmo clasifica todos los registros del dataset de entrenamiento. Para cada hoja, se utiliza la proporción...

K-Nearest Neighbors

Los KNN (K-Nearest Neighbors o K vecinos más cercanos) es un método especial que no crea un modelo como tal: el dataset de entrenamiento constituye el modelo. Este algoritmo se conoce como no paramétrico.

Cada dato se clasifica en función de los K datos más próximos en el espacio de variables. K es, por tanto, uno de los hiperparámetros que hay que determinar.

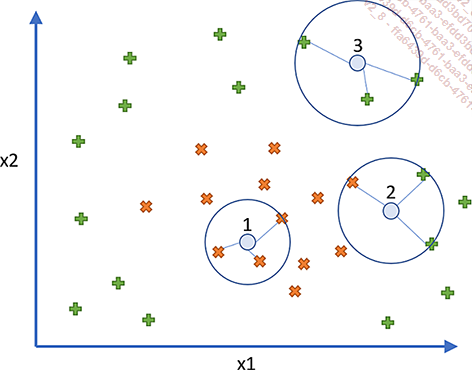
En el ejemplo de la gráfica anterior, dos clases están representadas por signos más (+) y los signos de cruz (X). Hay que predecir tres datos (círculos) y K se ha fijado en 3:

Círculo 1: los tres vecinos más próximos son X, por lo que el dato 1 se clasificará como X.
Círculo 2: los tres vecinos se dividen en dos + y una X, por lo que los datos se clasifican por mayoría como +.
Círculo 3: los tres vecinos son +, los datos se clasifican como +.

Si K es demasiado bajo, se seleccionarán pocos vecinos y el algoritmo será muy sensible a los casos especiales (sobreajuste). En cambio, si K es demasiado grande, los límites entre clases tenderán a desaparecer. Por convención, se elige K=5 de forma predeterminada antes de la optimización de los hiperparámetros, y se evitan los números pares porque pueden llevar a igualdades más fácilmente.

KNN es un algoritmo determinista: como las distancias no varían con el tiempo...

Logistic Regression

A pesar de su nombre, la regresión logística (logistic regression) es una técnica de clasificación, no de regresión. En el caso de la clasificación multiclase, se dice que es politómica.

1. Regresión logística binaria

La regresión logística funciona en dos etapas:

Crear una función lineal para las variables, que asocia los números positivos con los datos de la clase positiva y los valores negativos con los datos de la clase negativa.
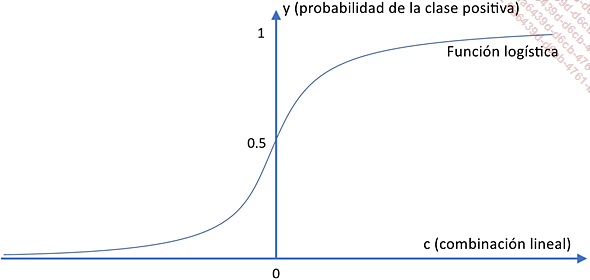
Aplicar la función logística al resultado obtenido para reducir la salida a un valor entre 0 y 1.

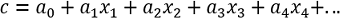La función lineal puede escribirse como images/ML6_9a.png

.

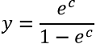La función logística puede escribirse como: images/ML6_9b.png

.

Para todos los valores negativos de c, y será inferior a 0,5 y, por tanto, se predecirá la clase negativa. Por el contrario, para los números positivos, se predice la clase positiva:

La regresión logística es fácil de configurar. El proceso de aprendizaje consiste en determinar los coeficientes de la función lineal. Para ello pueden utilizarse varias estrategias, denominadas «solucionadores» (solvers). Son iterativos y utilizan distintos algoritmos para intentar converger hacia el óptimo, es decir, el mejor conjunto de parámetros. Es habitual probar varios de ellos para obtener los mejores resultados.

También tiene la ventaja de ser fácil de entender. Cualquier variable con un coeficiente positivo indica una correlación positiva hacia la clase positiva. Un coeficiente negativo indica una correlación negativa.

Como los coeficientes también dependen de la escala de los datos de entrada, se recomienda encarecidamente utilizar la regresión logística después de normalizar las variables. Los coeficientes son entonces también comparables: la relación entre dos coeficientes da la importancia relativa de uno sobre el otro.

Por ejemplo, consideremos una regresión logística sobre tres variables y la función lineal:

c = 3x1 + 2x2 - x3

Las ponderaciones dadas a las variables son 3 para la variable x1, 2 para la variable...

Naive Bayes

1. Principio general

La clasificación bayesiana ingenua (Naive Bayes) toma su nombre de sus dos características principales:

Utiliza probabilidades condicionales (teorema de Bayes).
Hace una suposición denominada «ingenua» (naive), es decir, que las variables no están correlacionadas entre sí.

Esta técnica es fácil de utilizar y da buenos resultados de clasificación.

Las probabilidades condicionales corresponden al cálculo de P(B|A), la probabilidad de tener el suceso B sabiendo A. Por ejemplo, P(«Paraguas»|«Lluvia») indica la probabilidad de llevar un paraguas sabiendo que está lloviendo.

En el caso de la clasificación, lo que hay que determinar es la probabilidad de pertenecer a cada clase en función de las entradas. Esto se denomina P(y|X), es decir, la probabilidad de la clase y conociendo las entradas X.

Gracias al teorema de Bayes y al supuesto de que las variables son independientes entre sí, es posible calcular dicha probabilidad a partir de las probabilidades siguientes:

La probabilidad de y para el conjunto de la población (que generalmente corresponde a la proporción de datos de entrenamiento en la clase y). Es lo que se conoce como a priori.
La probabilidad de una característica para una clase determinada, que también puede verse como la proporción de cada valor de una variable para una clase determinada, por ejemplo, la proporción de individuos de 1ª clase que sobrevivieron. Esto se conoce como verosimilitud.
La probabilidad de tener las entradas X, es decir, la probabilidad de tener un caso así, se obtiene generalmente multiplicando las probabilidades de cada una de sus características en el conjunto de la población. Se conoce como evidencia.

La probabilidad de pertenecer a una clase determinada (también denominada posterior o a posteriori) se calcula mediante la fórmula:

Las clasificaciones bayesianas ingenuas no utilizan el azar. Es una técnica determinista, que siempre da el mismo resultado para el mismo dataset. Por lo tanto, no existe...

Support Vector Machine

1. Presentación general

Las Máquinas de Vectores de Soporte(SVM Support Vector Machine) son un conjunto de técnicas que generalizan los clasificadores lineales.

Combinan dos principios diferentes que, en conjunto, darán a las SVM toda su potencia.

a. Margen y soporte vectorial

En primer lugar, en el caso de un problema de clasificación linealmente separable, existe un número infinito de hiperplanos que pueden separar el espacio en dos. Intuitivamente, cuanto más alejado esté un límite de los puntos situados a ambos lados, más probable es que se generalicen bien nuevos puntos.

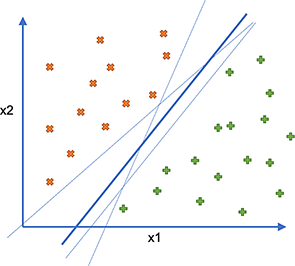
Así, en el ejemplo siguiente, las líneas finas son límites potenciales, pero permanecen cerca de ciertos puntos. En cambio, la línea más gruesa está lo más alejada posible de los distintos puntos, y sería un mejor clasificador.

En los ejemplos siguientes, utilizaremos solo ejemplos bidimensionales para mayor claridad. En la práctica, los problemas suelen tener muchas dimensiones. Por tanto, ya no se tratará de una línea divisoria, sino de un hiperplano, lo cual es una generalización matemática.

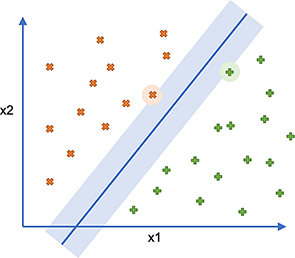
El margen de cada lado corresponde a la distancia entre la línea y el punto más cercano de cada clase. El primer punto del dataset que define el límite del margen se denomina «vector de soporte» (support vector) (de ahí el nombre SVM) y es el único que se debe conservar.

Otro nombre para SVM es separador de margen amplio, en referencia a esta búsqueda del margen máximo.

En el ejemplo, el margen se muestra como un rectángulo claro y los soportes están encerrados en un círculo:

Obviamente, un clasificador de este tipo rara vez es posible, ya que los límites suelen ser menos definidos de lo que son en este caso. Por lo tanto, existe un parámetro C que puede utilizarse para influir en el error aceptable al crear la separación, añadiendo una penalización a cada dato mal clasificado.

Cuanto menor sea la C, mayor será el error (la penalización sobre los errores es baja) pero mayor será el margen, lo que conduce a una mejor generalización. Por el contrario, una C grande significará una mejor clasificación en el conjunto de entrenamiento (debido a las grandes...

Algoritmos de clasificación