Metaheurísticos de optimización

Optimización y mínimos

Los problemas de optimización y de búsqueda de mínimos son comunes, y su resolución exacta es complicada, o incluso imposible. La inteligencia artificial ha desarrollado algoritmos específicos para estos problemas.

Algoritmos voraces

Los algoritmos voraces son los más sencillos. No construyen más que una única solución, pero de manera iterativa. Así, conforme avanza el tiempo, se agrega un elemento, el más prometedor.

Este algoritmo debe adaptarse a cada problema. Solo se mantiene el principio general.

De este modo, en el caso de la mochila, agregaremos conforme avancemos los objetos más interesantes hasta alcanzar la capacidad de la mochila.

Para ello, empezamos calculando el valor por kilo de cada objeto:

Ordenamos, a continuación, cada objeto desde el más interesante (el valor por kilo mayor) hasta el menos interesante. Se obtiene el orden siguiente:

A - D - K - I - L - B - C - E - J - H - F - G

Se parte de una mochila vacía. Se agrega el primer elemento tras la ordenación, en este caso el objeto A. La mochila contiene, ahora, 4 kg y posee un valor total de 15.

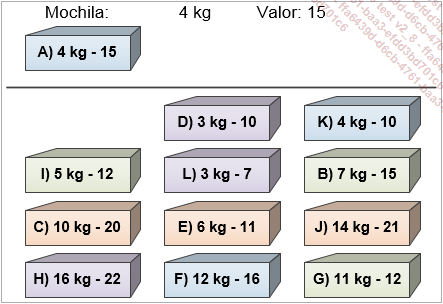
Se agrega, a continuación, el primer elemento de la lista ordenada restante. El objeto D no pesa más que 3 kg, de modo que es posible meterlo en la mochila.

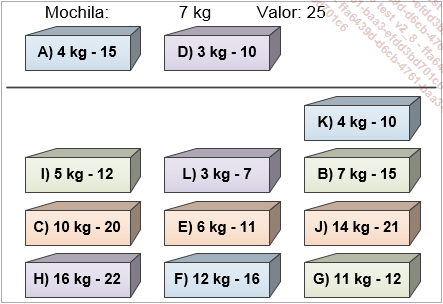
Esta contiene, ahora, 7 kg y posee un valor de 25. El siguiente elemento es K. Una vez se agrega, la mochila contiene 11 kg y posee un valor igual...

Descenso por gradiente

El descenso por gradiente es un metaheurístico incremental. A partir de una primera solución, escogida aleatoriamente o definida como base de partida (por ejemplo, la mejor solución conocida por los expertos), el algoritmo buscará una optimización sin modificar la solución más que en una unidad.

Cuando el problema es una función matemática, se calcula la derivada en el punto que representa la solución actual, y se sigue la dirección de la derivada más fuerte negativamente.

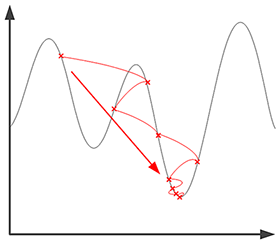
En el siguiente esquema, se indican las distintas soluciones obtenidas iterativamente: se parte de la solución más alta y se avanza en el sentido de la gradiente, hasta alcanzar el mínimo.

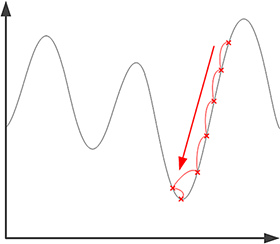
De manera intuitiva, este es el algoritmo utilizado por un senderista: si quiere alcanzar la cima de una montaña, pero no sabe dónde se encuentra, mira a su alrededor en qué dirección el camino sube más, y sigue dicha dirección. A fuerza de subir, se verá, necesariamente, en lo alto del macizo sobre el que se encuentre. El procedimiento es el mismo si quiere alcanzar el valle, siguiendo rutas descendientes.

Generalmente, la derivada...

Búsqueda tabú

La búsqueda tabú es una mejora de la búsqueda mediante descenso por gradiente. En efecto, esta última se bloquea en el primer óptimo encontrado.

En el caso de la búsqueda tabú, con cada iteración, nos desplazamos hacia el mejor vecino incluso aunque sea menos bueno que la solución actual. Además, se guarda una lista de las posiciones ya visitadas, que no se pueden seleccionar (de ahí el nombre: las anteriores soluciones se convierten en tabú).

De este modo, el algoritmo se "pasea" por el espacio de la solución y no se detiene en el primer óptimo descubierto. Se detendrá cuando todos los vecinos hayan sido visitados, tras un número máximo de iteraciones prefijado o cuando no se detecte ninguna mejora sustancial tras x pasos.

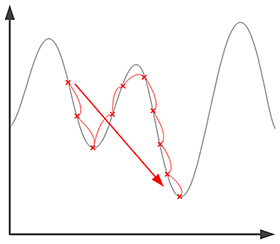
La principal dificultad de esta búsqueda es la elección de la longitud de la lista de posiciones tabú. En efecto, si esta lista es demasiado corta, corremos el riesgo de entrar en un bucle alrededor de las mismas posiciones. Por el contrario, una lista demasiado larga podría impedir probar otros caminos que partan de una misma solución potencial. No existe, sin embargo, ninguna manera de conocer la longitud de la lista ideal, debe seleccionarse de forma puramente empírica.

Esta lista se implementa, a menudo, como una fila (FIFO, del inglés First In First...

Recocido simulado

El recocido simulado mejora el descenso por gradiente y se inspira en el recocido utilizado en metalurgia. En efecto, cuando se están forjando o colando metales, estos sufren importantes restricciones. Es el caso de las hojas de las espadas, por ejemplo.

Para mejorar la duración del filo, se calienta la hoja (de ahí el nombre de recocido). De este modo, los átomos pueden cristalizarse en estructuras más resistentes, y disminuyen las restricciones mecánicas y térmicas. Las hojas de buena calidad sufren, de este modo, varios ciclos de calor y formado.

En informática, se va a utilizar este principio para mejorar las soluciones y salir de los óptimos locales. Se va a fijar una temperatura numérica, que disminuirá conforme pase el tiempo. Cuanto mayor sea esta temperatura, más grandes podrán ser los saltos en el espacio de búsqueda. Además se acepta, a diferencia de lo que ocurre con el descenso por gradiente, transitar soluciones menos óptimas que la solución actual.

El algoritmo empieza con una búsqueda global, y va a encontrar zonas más interesantes. Cuando la temperatura decrece, se va a concentrar en una zona concreta, y termina como una búsqueda por gradiente clásica. La probabilidad de encontrar el óptimo global y no un óptimo local es, por lo tanto, mayor.

Conforme avanza el tiempo, se comprueba...

Optimización por enjambre de partículas

En la mayoría de metaheurísticos, los resultados son mejores si se realizan varias ejecuciones a partir de soluciones iniciales diferentes. En efecto, esto permite recorrer una zona de búsqueda más amplia.

Sin embargo, es posible obtener varias veces la misma solución, y pasar por alto un óptimo global (o de un mejor óptimo local).

La optimización por enjambre de partículas se inspira en la biología. En efecto, tanto en el comportamiento de los pájaros como de los peces podemos observar grandes grupos de animales que se desplazan en conjunto en tres dimensiones. Los pájaros (o los peces) no se interfieren; sin embargo, la dirección de cada uno se adapta permanentemente en función de la dirección actual y la posición de los demás. Su velocidad también se adapta.

En este algoritmo, varias soluciones potenciales cohabitan en el espacio de búsqueda, y cada una se desplaza en una dirección determinada. Con cada iteración, las soluciones se van a desplazar como en una nube, avanzando hacia zonas que parezcan más interesantes.

Cada solución debe conocer su velocidad actual, según un vector (que permite indicar la dirección del desplazamiento) y las mejores posiciones descubiertas hasta el momento. Además, todas las soluciones del enjambre conocen la mejor...

Dominios de aplicación

Estos algoritmos resultan muy útiles en muchos dominios, en particular aquellos para los que no exista ninguna manera de calcular el óptimo de forma matemática o cuando esta actividad llevaría demasiado tiempo.

Obtienen un óptimo, local o global. Se espera, entonces, tener un resultado, si no es global, al menos el más cercano a su nivel de calidad.

Los encontramos, de este modo, en todos los dominios que realicen el diseño de piezas o de sistemas. En efecto, permiten encontrar fácilmente formas o materiales adecuados, limitando su coste (o, en función del problema, la superficie de rozamiento, las turbulencias...). Se utilizan en construcción, por ejemplo, para optimizar las estructuras de carga.

Se han realizado estudios para optimizar el coste de las estructuras de hierro en construcciones que tenían que respetar las normas antisísmicas.

En electrónica, sirven para mejorar el diseño de circuitos impresos, limitando la cantidad de "cable" necesario, o minimizando el espacio requerido por los diversos componentes.

En finanzas, los metaheurísticos permiten optimizar una cartera de acciones, limitando los riesgos y buscando maximizar las ganancias para una suma determinada.

Se utilizan en problemas de planificación como, por ejemplo, crear horarios de autobús/avión/tren. Se busca minimizar el coste para la empresa...

Implementación

En primer lugar, se implementan los algoritmos genéricos y, a continuación, se crean clases que heredan de las clases madres que permiten resolver el problema de la mochila.

Se utilizan dos versiones del problema de la mochila: la primera es la que se presenta como ejemplo en el algoritmo voraz (con 16 objetos), y la segunda es una versión más compleja y aleatoria, que permite comparar mejor los distintos algoritmos.

Se realiza un análisis de los resultados obtenidos al final de esta sección.

public interface Isolution  
{  
    double Value { get; }  
}
 

using System.Collections.Generic;  
   
public interface Iproblem  
{  
    List<ISolution> Neighbourhood(ISolution _currentSolution);  
   
    ISolution RandomSolution();  
   
    ISolution BestSolution(List<ISolution> _neighbours);  
}
 

using System;  
   
public interface IGUI  
{  
    void PrintMessage(String _message);  ...

Resumen

Este capítulo ha presentado cinco algoritmos clasificados como metaheurísticos. Todos ellos tienen como objetivo encontrar el óptimo de un problema. Si bien es preferible encontrar el óptimo global, cuando no existe ningún método matemático para obtenerlo y probar todas las soluciones sería demasiado largo, son la alternativa ideal permitiendo encontrar buenos óptimos locales, e incluso el óptimo global.

El primero es el algoritmo voraz. Consiste en construir de manera incremental una única solución, siguiendo lo que parece más adecuado para alcanzar un óptimo.

El descenso por gradiente parte de una solución aleatoria. En cada iteración, se analiza el vecindario de esta, y se sigue la dirección más prometedora. Cuando no se produce ninguna mejora en el vecindario, se ha alcanzado el óptimo local. Este algoritmo es simple y funciona bien, aunque a menudo se queda bloqueado en los óptimos locales y no encuentra, necesariamente, el óptimo global.

La búsqueda tabú se ha creado para permitir mejorar el descenso por gradiente. En efecto, en lugar de desplazarse de una posición a otra siguiendo una progresión, se desplaza hasta el mejor vecino accesible, mejor o no que nosotros. Así, no se queda atrapado en óptimos locales. Además, para evitar encontrar regularmente las mismas posiciones...