Búsqueda de rutas
Presentación del capítulo
Muchos dominios se enfrentan a un problema de búsqueda de rutas, denominada pathfinding en inglés. Recordamos, en primer lugar, los GPS y los programas de búsqueda de itinerarios (en coche, en tren, en transporte público...), también los videojuegos en los que los enemigos deben alcanzar al jugador por la ruta más corta.
La búsqueda de rutas es, en realidad, un dominio más bien vasto. En efecto, muchos problemas pueden representarse bajo la forma de un grafo, como la sucesión de movimientos en un juego de ajedrez.
La búsqueda de una ruta puede verse, en este caso, como la búsqueda de la serie de movimientos que se deben realizar para ganar.
Este capítulo presenta, en primer lugar, los distintos conceptos de la teoría de grafos y las definiciones asociadas. A continuación, se presentan los algoritmos fundamentales con su funcionamiento y sus restricciones.
Más adelante, se exponen los principales dominios en los que se puede utilizar esta búsqueda de rutas y se presenta un ejemplo de implementación de estos algoritmos en C#, aplicado a una búsqueda de rutas en un entorno en 2D.
El capítulo termina con un resumen.
Rutas y grafos
Una ruta puede verse como un recorrido por un grafo. Los principales algoritmos se basan, por lo tanto, en la teoría de grafos.
1. Definición y conceptos
Un grafo es un conjunto de nodos o vértices (que pueden representar, por ejemplo, ciudades) ligados por arcos, que serán las rutas.
He aquí un grafo que representa las estaciones y los vínculos que existen entre ellas (en tren, sin trasbordo):
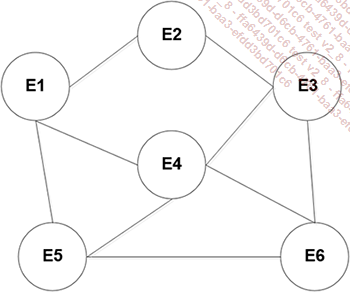
Las estaciones E1 a E6 son los nodos. El arco que va de E5 a E6 indica la presencia de un enlace directo entre estas dos estaciones. Se escribe (E5, E6) o (E6, E5) según el sentido deseado.
Por el contrario, para ir de E1 a E6 no existe ningún enlace directo. Será preciso pasar por E4 o por E5 si se desea realizar un único trasbordo, o por E2 y, a continuación, por E3 con dos trasbordos.
Una ruta permite alcanzar varios destinos unidos entre sí mediante arcos. De este modo, E1-E2-E3-E6 es una ruta de distancia 3 (la distancia es el número de arcos seguidos).
Hablamos de circuito cuando es posible partir de un nodo y volver a él. Aquí, el grafo contiene varios circuitos, como por ejemplo E1-E4-E5-E1 o E4-E5-E6-E4.
El orden de un grafo se corresponde con el número de destinos que contiene. Nuestro ejemplo contiene 6 estaciones, se trata por tanto de un grafo de orden 6.
Dos nodos se dice que son adyacentes (o vecinos) si existe un vínculo que permite...
Ejemplo en cartografía
Para estudiar los distintos algoritmos, vamos a interesarnos en un pequeño juego en el que controlamos a un personaje que representa un explorador. Como en muchos juegos de rol, nuestro héroe está limitado en cada turno (no tiene derecho más que a cierto número de puntos de acción). Para ir lo más rápido posible desde un punto a otro, buscaremos la ruta más corta en el mapa, teniendo en cuenta el tipo de terreno.
Existen varias formas, que requieren más o menos energía (y por consiguiente, puntos de acción):
-
Caminos, que requieren un punto de acción por casilla.
-
Hierba, que requiere dos puntos de acción.
-
Puentes, que requieren dos puntos de acción.
-
Agua, infranqueable.
-
Árboles, infranqueables también.
El mapa es el siguiente:
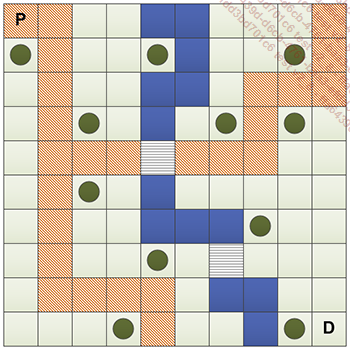
Y la leyenda:

Vamos a buscar la ruta que permita ir desde el punto de partida (P) hasta el destino (D), utilizando la menor cantidad posible de puntos de acción. La ruta más corta cuesta 27 puntos de acción (siguiendo la ruta y pasando el primer puente; a continuación, acortando por hierba hasta el final).
Algoritmos exhaustivos de búsqueda de rutas
Estos primeros algoritmos no son "inteligentes": se denominan exhaustivos, puesto que no utilizan ningún conocimiento relativo al problema para proceder. En el peor de los casos, comprueban todas las rutas posibles para determinar si existe alguna ruta entre ambos nodos.
Además, nada indica que la ruta encontrada sea la más corta. Sin embargo, son muy fáciles de implementar.
1. Búsqueda en profundidad
Se trata del algoritmo que probamos de manera natural en un laberinto: buscamos avanzar lo más rápido posible y, si nos bloqueamos, volvemos a la última intersección que hemos encontrado y probamos una nueva ruta.
Este algoritmo no permite determinar el camino más corto, sino simplemente encontrar un camino.
a. Principio y pseudo-código
Su funcionamiento es bastante sencillo.
En primer lugar, seleccionamos el orden en que recorreremos los nodos y, a continuación, aplicaremos este orden para avanzar lo máximo posible. Si nos bloqueamos, volvemos atrás, y probamos la siguiente posibilidad.
El recorrido en profundidad permite, por tanto, determinar la existencia de una ruta, pero no tiene en cuenta la longitud de los arcos, y por tanto no permite saber si se ha encontrado el camino más corto.
Además, el resultado obtenido depende en gran medida del orden escogido para recorrer el grafo, el orden óptimo depende de cada problema y no puede determinarse a priori. A menudo, no es eficaz. En el peor de los casos, debe comprobar todas las posibilidades para encontrar un camino.
Es, sin embargo, muy fácil de implementar. En efecto, vamos a conservar una lista de los nodos visitados. Cada vez que nos encontremos sobre un nodo, vamos a agregar todos sus vecinos no visitados a una pila en el orden seleccionado. A continuación, extraeremos el primer elemento de la pila.
Una pila (o LIFO, del inglés Last In, First Out) es una estructura algorítmica en la que los elementos se agregan en la parte superior y se extraen partiendo de la parte superior, como una pila de platos, de papeles... No es posible extraer un elemento de la mitad de la pila. Agregar un elemento por encima se denomina apilar, y extraerlo se dice desapilar.
Para facilitar la reconstrucción del camino obtenido, se conserva el predecesor de cada nodo...
Algoritmos "inteligentes"
Las búsquedas en profundidad y en anchura no permiten encontrar el camino más corto, aunque sí el primero que permite alcanzar el punto de destino desde el punto de partida.
Existen otros algoritmos que permiten determinar el camino más corto, o al menos un camino optimizado, sin tener que comprobar necesariamente todas las rutas posibles.
1. Algoritmo de Bellman-Ford
El algoritmo de Bellman-Ford permite encontrar el camino más corto, si existe. No es el óptimo, pero es el que funciona en la mayoría de casos. En efecto, permite definir longitudes negativas para los arcos, y no solamente positivas.
Además, si hay algún circuito cuya longitud sea negativa (y, por tanto, que permita disminuir el peso total), es capaz de detectarlo. Esto es importante, pues en este caso no existe ruta más corta.
a. Principio y pseudo-código
Este algoritmo va a utilizar la matriz de longitudes. Su funcionamiento es iterativo.
Al principio, se inicializa a +∞ la longitud mínima de cada nodo (lo que significa que no se ha encontrado todavía ningún camino hasta allí desde el destino). Se va a guardar, también, para cada nodo el nodo anterior (el que permite llegar a él de la manera óptima en longitud) e inicializarlo con un nodo vacío.
Se aplica, a continuación, tantas veces como número de nodos menos 1 mida el mismo bucle. De este modo, si tenemos 7 nodos, se aplica 6 veces.
Con cada iteración, se sigue cada arco (u,v). Se calcula la distancia desde el punto de partida hasta v como la distancia del inicio hasta u más la longitud del arco (u,v). Se obtiene, también, una nueva longitud para ir hasta el nodo v que comparamos con la que ya tenemos registrada. Si esta longitud es mejor que la obtenida hasta el momento, se cambia la longitud de este nodo y se indica que su predecesor es ahora u.
Solo deben utilizarse los arcos que parten de un nodo cuya distancia calculada es diferente de +∞. En efecto, en caso contrario se guarda una distancia infinita, que no puede mejorar las rutas que ya se han encontrado.
Si en una iteración no hay ningún cambio, puesto que ningún arco permite encontrar una distancia menor que la conocida, podemos detener prematuramente el algoritmo.
Además, si se aplica el algoritmo tantas veces como números de nodos...
Dominios de aplicación
Estos algoritmos de búsqueda de rutas se utilizan en muchos dominios.
El primer dominio es el de la búsqueda de itinerarios. Todos los GPS y las aplicaciones que permiten ir desde un lugar a otro (en tren, en bus, en metro, a pie...) utilizan algoritmos de pathfinding. Tienen en cuenta la longitud del camino o su tiempo. Vista la complejidad de los mapas que a menudo se utilizan (por ejemplo, en Google Maps), resulta evidente que los algoritmos deben optimizarse, dando preferencia a los grandes ejes siempre que sea posible. El detalle de los algoritmos obviamente no se ha expuesto.
Esta búsqueda de rutas se encuentra en los videojuegos. El objetivo es desplazar a un personaje (controlado por el jugador o representando a un enemigo) desde un lugar a otro. Los mapas pueden ser muy grandes, y el número de personajes importante. En este caso, conviene optimizar los algoritmos utilizados. Podemos destacar, sin embargo, que el algoritmo A* es el más implementado.
La robótica es otro campo que utiliza la búsqueda de itinerarios. Se trata de llevar a un robot de un punto a otro lo más rápido posible. Estos algoritmos se modifican, generalmente, por dos motivos. El primero es que el entorno fluctúa: si el robot avanza entre humanos, estos se desplazarán y le bloquearán el camino o, por el contrario, le despejarán rutas. Es preciso, por tanto, recalcular permanentemente...
Implementación
Vamos a pasar a la implementación de estos algoritmos. El código será, sin embargo, muy genérico, lo que permitirá fácilmente agregar nuevos métodos de resolución o nuevos problemas para resolver.
A continuación, lo aplicaremos al problema del mapa, mediante una aplicación de consola.
1. Nodos, arcos y grafos
La primera etapa consiste en definir nuestros grafos. Vamos a empezar por los nodos; a continuación, veremos los arcos que los enlazan y, por último, el grafo completo.
a. Implementación de los nodos
Los nodos son las estructuras básicas de nuestros grafos. Sin embargo, el contenido real de un nodo depende en gran medida del problema que se desea resolver: puede tratarse de estaciones, de casillas en una cuadrícula, de servidores, de ciudades...
Creamos, por tanto, una clase abstracta Node, que contendrá la información necesaria para los algoritmos. Esta clase debe ser heredada para la resolución práctica de un problema.
Los nodos necesitan tres datos:
-
El precursor, que es también un nodo.
-
La distancia desde el inicio.
-
La distancia estimada hasta el destino (si es necesario).
Utilizaremos propiedades. En el caso de las dos primeras, poseen valores por defecto.
public abstract class Node
{
private Node precursor = null;
internal Node Precursor
{
get
{
return precursor;
}
set
{
precursor = value;
}
}
private double distanceFromBeginning = double.PositiveInfinity;
internal double DistanceFromBeginning
{
get
{
return distanceFromBeginning;
}
...Resumen
La búsqueda de rutas, o pathfinding, permite vincular los nodos de un grafo utilizando arcos predefinidos. Estos están asociados a una longitud (o coste). Es posible, también, buscar la ruta con el menor coste, siendo el coste un kilometraje, un tiempo o incluso un precio (por ejemplo, la gasolina consumida).
Existen varios algoritmos, cada uno con sus particularidades.
Cuando se intenta saber si existe un camino, sin buscar el más corto, podemos utilizar algoritmos de búsqueda exhaustiva en profundidad o en anchura. Si se sabe, de manera global, en qué dirección ir, la búsqueda en profundidad puede resultar interesante (siempre que se le precise bien el orden para recorrer los nodos vecinos).
La búsqueda en anchura produce, generalmente, mejores resultados y es, sobre todo, más genérica. En ambos casos, se avanza de nodo en nodo y se memorizan los nodos adyacentes descubiertos, que visitaremos posteriormente. Se diferencian en la estructura utilizada para almacenar los nodos vecinos: una pila para la búsqueda en profundidad y una cola para la búsqueda en anchura.
El algoritmo de Bellman-Ford permite encontrar el camino más corto, sea cual sea el grafo. Consiste en aplicar los arcos para calcular las distancias óptimas mediante numerosas iteraciones. No es rápido realizando cálculos, pero es fácil de implementar, y puede resultar eficaz puesto...
 Ediciones ENI Editorial | líder en informática
Ediciones ENI Editorial | líder en informática

