Ediciones ENI Editorial | líder en informática
Lógica difusa
Presentación del capítulo
La lógica difusa es una técnica de inteligencia artificial determinista que permite tomar decisiones. Permite, también, obtener un comportamiento coherente y reproducible en función de las reglas que se le proveen. La inteligencia de esta técnica se encuentra en su capacidad de gestionar la imprecisión y presentar un comportamiento más flexible que un sistema informático tradicional.
Este capítulo empieza definiendo la noción de imprecisión, para no confundirla con incertidumbre. A continuación, se abordan los distintos conceptos: los conjuntos difusos, las funciones de pertenencia y los distintos operadores en lógica difusa.
La siguiente sección aborda las reglas difusas y los pasos para aplicar estas reglas a un caso concreto y obtener un resultado utilizable (se denominan, respectivamente, fuzzificación y defuzzificación).
El capítulo continúa con la presentación de diversos dominios de aplicación de la lógica difusa, que encontramos actualmente desde en nuestras lavadoras hasta en nuestros coches, pasando por los motores.
Para terminar, la última sección consiste en mostrar cómo puede implementarse un motor de lógica difusa genérico y evolutivo en Java. Se detallan las diferentes clases y puede descargarse el código completo. Se provee, también...
Incertidumbre e imprecisión
Es muy importante distinguir dos conceptos: incertidumbre e imprecisión. En efecto, cada uno va a estar asociado a una técnica de inteligencia artificial diferente.
1. Incertidumbre y probabilidad
La incertidumbre es, evidentemente, lo contrario de la certidumbre. Por ejemplo, la regla "Si va a llover, entonces cogeré el paraguas" es segura (al 100 %): mojarse no resulta agradable. Por el contrario, el enunciado "Mañana debería llover" es incierto: el parte meteorológico ha podido anunciar lluvias, pero nada obliga a que tenga que llover necesariamente. Podríamos decir que la probabilidad de que llueva es del 80 %, por ejemplo. Cualquier enunciado cuya probabilidad sea diferente del 100 % es incierto.
2. Imprecisión y subjetividad
Por el contrario, la imprecisión se manifiesta cuando falta... ¡precisión! En los hechos, esto se traduce en enunciados que resulta difícil evaluar: parecen subjetivos. Por ejemplo, en la frase "Si hace mucho calor, entonces no cogeré chaqueta", la imprecisión se sitúa en la expresión "mucho calor".
Es cierto que si hace "mucho calor" no cogeré la chaqueta, en cuyo caso no hay incertidumbre. Pero ¿hace mucho calor a 35º? Probablemente sí. ¿Y a 30º? De algún modo, podríamos afirmar que hace "mucho...
Conjuntos difusos y grados de pertenencia
Si retomamos el ejemplo de nuestra persiana eléctrica y la temperatura, nos gustaría definir el término "calor". Vamos a definir, por tanto, para qué temperaturas hace calor o no.
1. Lógica booleana y lógica difusa
En lógica booleana (la lógica clásica), un valor puede ser solamente verdadero o falso. Se debe definir un valor preciso que sirve de transición. Para definir "caliente" en nuestra persiana, este valor es 25º. Por encima de esta temperatura, "calor" es verdadero, y por debajo, "calor" es falso. No existen valores intermedios.
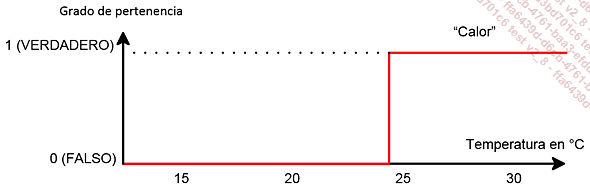
En lógica difusa, utilizaremos un conjunto difuso. Se diferencia de un conjunto booleano por la presencia de una "fase de transición", durante la cual la variable se sitúa entre los valores verdadero y falso. Para temperaturas entre 20º y 25º, hará más o menos calor.
Por debajo de los 20º, diremos que no hace calor, y por encima de los 25º, diremos que hace calor en un 100 %. Pero, a 23º, no hace calor más que en un 60 % (es decir, un 0.6).
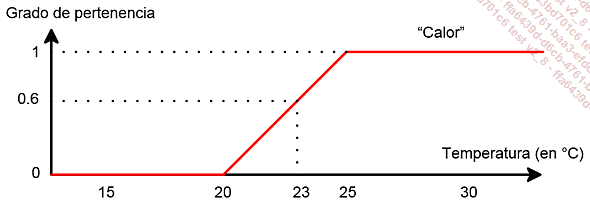
2. Funciones de pertenencia
Vemos, así, como en la lógica booleana se trabaja únicamente con los términos "verdadero" o "falso". Se pasa de falso (0 %) a verdadero (100 %) a 25º. En lógica difusa, se agregan etapas intermedias: entre 20º y 25º se pasa, progresivamente, de falso a verdadero. De esta manera, es posible leer en el gráfico que el grado de pertenencia (o valor de verdad) de "calor" para una temperatura de 23º es de 0.6, es decir, un 60 %. De forma similar, a 24º, hace calor en un 80 %.
La curva que indica los grados de pertenencia...
Operadores sobre los conjuntos difusos
En lógica clásica, existen tres operadores de composición elementales: la unión (O), la intersección (Y) y la negación (NO). Estos operadores son también necesarios en lógica difusa, en particular para poder componer valores lingüísticos (por ejemplo, "fresco O bueno") y escribir reglas.
1. Operadores booleanos
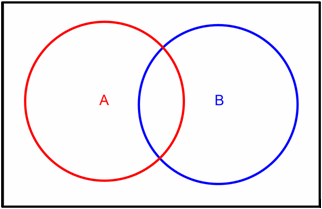
En lógica booleana, estos tres operadores pueden representarse gracias a diagramas de Venn. En ellos, los conjuntos se representan mediante círculos.
Aquí vemos dos conjuntos, A y B, que se superponen en parte:
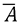. Representa el conjunto de valores que no pertenecen
a A. Se representa mediante la zona sombreada:
B. Representa el conjunto de valores que pertenecen
a uno u otro conjunto. Aquí se representa mediante la zona
sombreada:
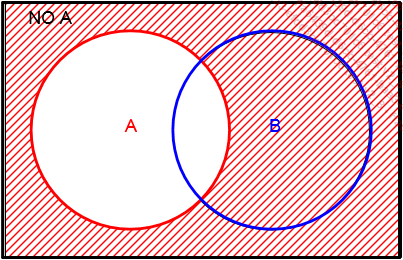
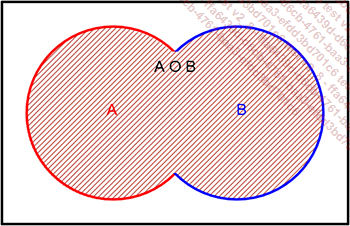
B; representa el conjunto de valores que pertenecen
a ambos conjuntos al mismo tiempo. Se representa aquí mediante
la zona sombreada común a ambos conjuntos: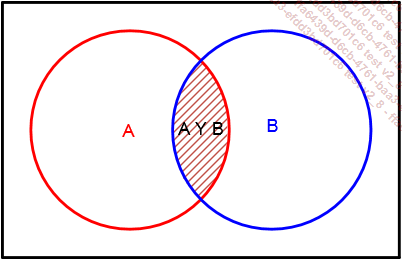
2. Operadores difusos
En lógica difusa, no hay una transición clara entre lo que es falso y lo que es verdadero. Los operadores clásicos no pueden, por lo tanto, aplicarse y los diagramas de Venn no están bien adaptados....
Creación de reglas
1. Reglas en lógica booleana
En un sistema clásico, como el control de la persiana del principio de este capítulo, una regla se expresa de la siguiente manera:
SI (condición precisa) ENTONCES acción Por ejemplo:
SI (temperatura ≥ 25°) ENTONCES bajar la persiana Podemos diseñar reglas más complejas. Por ejemplo, podríamos tener en cuenta la claridad exterior, que se mide en lux (puesto que si hace sol conviene protegerse). Va desde 0 (noche negra sin estrellas ni luna) hasta más de 100 000 (claridad directa del sol). Un cielo nublado de día se corresponde con una claridad entre 200 y 25 000 lux aproximadamente (en función de la densidad de las nubes).
En nuestra aplicación de control de la persiana, podríamos crear la siguiente regla:
SI (temperatura ≥ 25° Y claridad ≥ 30 000 lux) ENTONCES bajar la persiana Esto plantea, sin embargo, problemas cuando la temperatura medida o la claridad están cerca de los valores límites.
2. Reglas difusas
En un sistema difuso, las reglas utilizan valores difusos en lugar de valores numéricos. La notación de las expresiones utilizadas en las reglas sigue la forma:
"Variable lingüística" ES "valor lingüístico" Vamos a definir tres variables lingüísticas: la temperatura, la claridad y la altura de la persiana.
Empezamos...
Fuzzificación y defuzzificación
1. Valor de verdad
Las distintas reglas poseen, todas, una implicación (la cláusula ENTONCES). Será preciso expresar hasta qué punto la regla debe aplicarse, en función de los valores numéricos medidos: es la etapa de fuzzificación.
Nos centraremos en la regla R8:
SI temperatura ES buen tiempo Y claridad ES media ENTONCES persiana ES
a media altura Queremos saber hasta qué punto se aplica esta regla para una temperatura de 21 ºC y una claridad de 80 000 lux.
Buscaremos, en primer lugar, hasta qué punto hace "BUEN TIEMPO". La siguiente figura nos indica que a 21 ºC hace buen tiempo al 80 %.
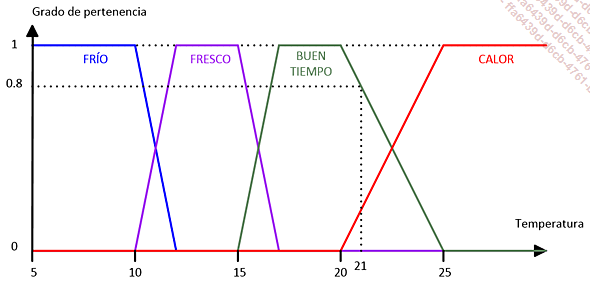
Buscaremos, a continuación, hasta qué punto la claridad es MEDIA para 80 000 lux. Podemos comprobar que está al 25 %:
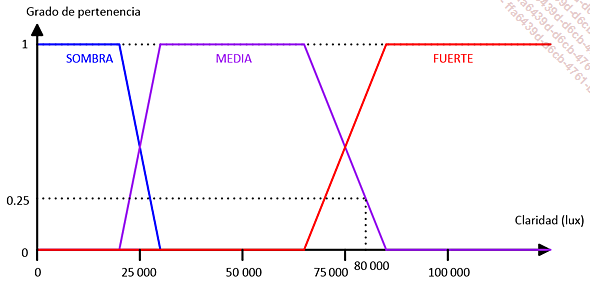
La regla contiene, por lo tanto, una parte verdadera al 80 % y una parte verdadera al 25 %. Diremos que la regla entera es verdadera al 25 %, el valor mínimo (operador Y). Es el término menos verdadero el que determina el valor de la verdad de una regla completa.
2. Fuzzificación y aplicación de las reglas
Buscaremos ahora saber cuál será el resultado de esta regla. Nos dice que la persiana debe estar a media altura. Sabemos que la regla se aplica en un 25 %.
Tenemos muchas opciones para el operador de implicación a fin de determinar el conjunto difuso resultante. Nos interesaremos en dos de ellos: la implicación de Mamdani y la de Larsen. Lo que cambia entre ambas es la forma del conjunto difuso obtenido.
Para el operador de implicación de Mamdani...
Dominios de aplicación
Zadeh expuso las bases teóricas de la lógica difusa en 1965. Los países occidentales no se interesaron realmente por esta técnica en sus inicios. Por el contrario, Japón comprendió rápidamente su interés, seguido algunos años más tarde por el resto del mundo.
1. Primer uso
En 1987, el primer tren controlador por un sistema basado en reglas difusas apareció en Sendai, una ciudad a menos de 400 km al norte de Tokio. Los ingenieros quisieron maximizar el confort de los viajeros minimizando el consumo de energía, de modo que el vehículo debía realizar numerosos cambios de velocidad. La velocidad del tren es, por tanto, resultado de la lógica difusa.
Se ha demostrado que el consumo de energía disminuyó en un 10 % respecto a un conductor humano, y que los pasajeros elogiaban la suavidad en la conducción, principalmente en los arranques y las paradas.
Está todavía en circulación y ha supuesto el primer gran éxito comercial de la lógica difusa.
2. En los productos electrónicos
Muchos otros constructores comprendieron que un controlador difuso podía mejorar el funcionamiento de las máquinas que lo contenían.
Es así como actualmente estamos envueltos de lógica difusa, sin ni siquiera saberlo: encontramos ejemplos en las lavadoras de la marca LG (para seleccionar...
Implementación de un motor de lógica difusa
Esta sección describe cómo codificar un motor de lógica difusa, utilizando las premisas expuestas hasta el momento. El siguiente código está escrito en Java, pero podría adaptarse fácilmente a cualquier otro lenguaje orientado a objetos. Utiliza Java 10, aunque no necesita librerías externas para una mejor portabilidad.
Cuando se requieran conocimientos matemáticos, se explicarán las fórmulas utilizadas.
1. El núcleo del código: los conjuntos difusos
a. Punto2D: un punto de una función de pertenencia
Vamos a comenzar creando las clases básicas. Para ello, necesitaremos una clase Punto2D que nos permita definir las coordenadas de un punto representativo de las funciones de pertenencia. El eje de abscisas (x) representa el valor numérico y el eje de ordenadas (y) el valor de pertenencia correspondiente, entre 0 y 1.
La base de esta clase es la siguiente:
public class Punto2D {
// Coordenadas
public double x;
public double y;
// Constructor
public Punto2D(double _x, double _y) {
x = _x;
y = _y;
}
} Más adelante, habrá que comparar dos puntos para conocer su orden. En lugar de comparar nosotros mismos las coordenadas x de los puntos, vamos a implementar la interfaz Comparable en esta clase. Modificaremos el encabezado de la siguiente manera:
public class Punto2D implements Comparable A continuación, es preciso agregar el método compareTo, que permite saber si el punto que se pasa como parámetro es más pequeño, igual o más grande en relación con el objeto en curso (el método debe devolver, respectivamente, un número positivo, cero o negativo). Nos contentaremos con calcular la diferencia de las abscisas:
@Override
public int compareTo(Object t) {
return (int) (x - ((Punto2D) t).x);
} Por último, el método toString() permite facilitar la visualización:
@Override
public String toString() {
return "(" + x + ";" + y + ")";
} b. ConjuntoDifuso: un conjunto...
Implementación de un caso práctico
Vamos a utilizar la lógica difusa para controlar el GPS de un coche, y en particular su nivel de zoom. En efecto, en función de la distancia al próximo cambio de dirección y de la velocidad a la que se circule, el nivel de zoom no es el mismo: cuando nos aproximamos a un cambio de dirección o disminuimos la velocidad, el zoom aumenta para mostrarnos el mapa con un mayor nivel de detalle.
Para obtener una visualización difusa y no entrecortada, se utiliza un controlador difuso. Para ello, creamos en primer lugar una nueva clase que contiene de momento un único método main:
public class ZoomGPS {
public static void main(String[] arg) {
System.out.println("Lógica difusa: caso del zoom de un GPS");
// Aquí el código
} Creamos, en primer lugar, un nuevo controlador difuso:
// Creación del sistema
ControladorDifuso controlador = new ControladorDifuso("Gestión del zoom de un GPS"); La siguiente etapa consiste en definir las distintas variables lingüísticas. En nuestro caso tendremos tres: Distancia y Velocidad como entrada, y Zoom como salida. Para la distancia (medida en metros hasta el siguiente cambio de dirección), crearemos tres valores lingüísticos: "Pequeña", "Media" y "Grande".
He aquí el esquema que representa estos conjuntos difusos:
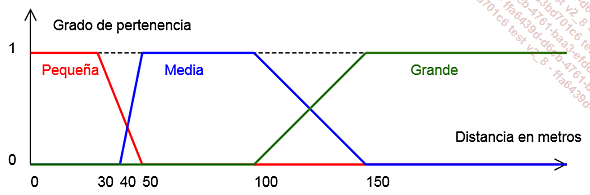
En el código, crearemos la variable lingüística Distancia, y a continuación le agregaremos los tres valores lingüísticos; por último, agregaremos esta variable como entrada al sistema:
System.out.println("Agregar las variables de entrada");
// Variable lingüística de entrada:
// distancia (en m, de 0 a 500 000)
VariableLinguistica distancia = new
VariableLinguistica("Distancia", 0, 500000);
distancia.AgregarValorLinguistico(new
ValorLinguistico("Pequeña", new ConjuntoDifusoTrapecioIzquierda(0,
500000, 30, 50)));
distancia.AgregarValorLinguistico(new ...Resumen
La lógica difusa permite tomar decisiones en función de reglas poco precisas, es decir, cuya evaluación esté sometida a cierta interpretación.
Para ello, se definen variables lingüísticas (como la temperatura) y se les asocia valores lingüísticos ("calor", "frío"...). A cada valor se le hace corresponder un conjunto difuso, determinado por su función de pertenencia: para todos los valores numéricos posibles, se asocia un grado de pertenencia entre 0 (el valor lingüístico es totalmente falso) y 1 (es totalmente verdadero), pasando por estados intermedios.
Una vez definidas las variables y los valores lingüísticos, se indican al sistema difuso las reglas que hay que aplicar. Se le indican, a continuación, los valores numéricos medidos.
La primera etapa para proporcionar una decisión es la fuzzificación, que consiste en asociar a cada valor numérico su grado de pertenencia a los distintos valores lingüísticos. A continuación se pueden aplicar las reglas, y la suma de las reglas (constituida por la unión de los conjuntos difusos resultantes) proporciona un nuevo conjunto difuso.
La defuzzificación es la etapa que permite pasar de este conjunto difuso al valor numérico que representa la decisión final. Existen varios métodos para llevar a cabo esta tarea, aunque...
