Pasar al modo confirmado

1. Implementación de la memoria

Cuando ejecutamos un programa en un ordenador, éste tiene que almacenar toda la información para que el programa se ejecute correctamente. Para almacenar los datos durante la ejecución, utiliza una zona de memoria dedicada, su pila (o stack en inglés).

La pila funciona como una pila de objetos en la vida real: podemos recuperar un objeto de la pila empezando por el objeto situado en la parte superior, es decir, el último objeto colocado en la pila. Por tanto, el primer objeto de la pila es el último que podemos recuperar.

La pila no puede recordar un elemento concreto porque se van desapilando, es decir, eliminando de la pila, a medida que se ejecuta el programa. Este sistema permite a la pila ejecutar instrucciones con extrema rapidez porque no retiene nada.

Podemos pensar en esta pila como un espacio compacto en el que cada celda tiene un tamaño fijo en bytes y, sobre todo, un número fijo de celdas para simplificar su implementación.

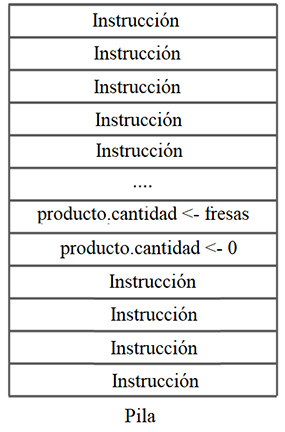
Pila utilizada durante la ejecución de un programa

Consideremos un ejemplo sencillo con nuestra estructura de datos que representa los productos de una lista de la compra. En la figura anterior, podemos ver que esta estructura ocupará dos casillas. Pero, ¿no representan estas celdas una única variable?

2. Gestión de punteros

Para ahorrar espacio en la pila y recuperar elementos específicos...

1. Listas enlazadas simples

Las primeras listas son las listas enlazadas simples. Este tipo de listas solo se pueden leerse desde el primer enlace hasta el último.

A diferencia de las tablas, no existe el operador de indexación [ ], sea cual sea el tipo de lista. El acceso a una lista solo es secuencial: cada enlace lleva al siguiente, empezando siempre por el primero.

a. Creación

Para crear una lista simple enlaza, primero tenemos que representar qué es un enlace. Para ello, vamos a utilizar una ESTRUCTURA que contenga dos campos, como se muestra en la siguiente figura:

• El valor de los datos.

• El puntero al siguiente enlace.

Representación de una lista enlazada simple

Para indicar que el enlace es el último de la lista, el siguiente campo apuntará al valor NULL.

ESTRUCTURA enlace  
INICIO  
   valor : tipo  
   *siguiente <- NULL : enlace  
FINESTRUCTURA 

Al igual que las tablas, las listas solo pueden contener valores del mismo tipo, como muestra el enlace ESTRUCTURA. Suponemos que cada enlace creado será el último, de ahí la inicialización del siguiente puntero a NULL, es decir, el último elemento de la lista.

Utilizando la ESTRUCTURA enlazada, ahora podemos definir la ESTRUCTURA lista, que se muestra en la figura anterior:

ESTRUCTURA lista ...

1. Aspectos principales

En realidad, un árbol en algoritmia se inspira en los árboles de la naturaleza. Son estructuras formadas por una raíz, el punto de acceso y ramas y hojas, los puntos intermedios y terminales. Solo podemos recorrer un árbol partiendo de la raíz. Cada rama se puede considerarse un subárbol, como se ilustra en la figura siguiente, con su raíz y sus ramas. Esta definición nos da una idea clara de una estructura que utiliza la recursividad.

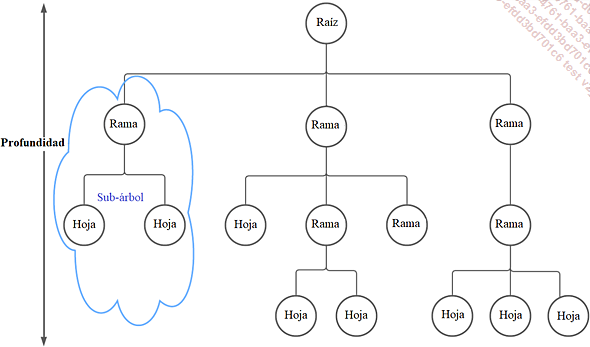
Un árbol cualquiera

Nosotros también utilizamos árboles en nuestras vidas. El ejemplo más evidente de esta estructura compleja es el árbol genealógico.

2. Creación

El árbol se crea utilizando una estructura de datos compleja que, al igual que la lista, se construye sobre otra ESTRUCTURA: los nodos. Un nodo de un árbol puede ser la raíz, una rama o una hoja. Por tanto, cada nodo tendrá una lista de otros nodos, excepto las hojas, que serán una lista vacía.

Por tanto, un árbol vacío es una ESTRUCTURA que contiene un puntero a un nodo inicializado en NULL.

Cada árbol tiene también una característica que describe su número de niveles: su profundidad. Podemos simplificar la profundidad diciendo el número de veces que podemos bajar por el árbol. Por ejemplo, el árbol de la figura anterior tiene una profundidad de tres. Un árbol con una sola raíz tendría una profundidad de cero.

En esta sección, nos centraremos únicamente en los aspectos principales de los árboles y su manipulación, dado que un nodo puede tener un número máximo ilimitado de nodos bajo él. Por razones pedagógicas, la parte algorítmica se tratará en la siguiente sección, cuando hablemos de un tipo específico de árbol: los árboles binarios.

Veamos ahora los diferentes recorridos de los árboles.

3. Recorrido a lo ancho

El recorrido a lo ancho de un árbol consiste en recorrerlo por niveles. Empezamos por la raíz, después las ramas de la raíz, continuamos con las ramas de las ramas, y así sucesivamente hasta llegar a las hojas.

La anchura del árbol que se muestra en la figura siguiente será la siguiente: A B E K C D F G J L H I M N y Z para terminar....