Condiciones, pruebas y buleanos

1. Las condiciones son esenciales

En nuestra vida, nuestro comportamiento se rige por una multitud de decisiones que debemos tomar. Volviendo al ejemplo del paso de peatones, cruzaremos si el semáforo de peatones está en verde, de lo contrario esperaremos si está en rojo. Lo mismo ocurre con los algoritmos y los programas: tenemos que guiar al ordenador para que tome las decisiones adecuadas y ejecute correctamente nuestras instrucciones.

Recuerde que hay que explicárselo todo a la máquina, nunca tomará una decisión por sí sola, salvo quizás apagarse en caso de cortocircuito. Hay que indicarle al ordenador cuándo puede llevar a cabo las instrucciones. Por ejemplo, como cuando un adulto enseña a dibujar a un niño pequeño: el adulto enseña al niño cómo coger el lápiz, cuál es el extremo adecuado para dibujar, que solo se puede dibujar sobre una hoja de papel y no sobre una mesa o una pared, etc. La ventaja de la programación para nosotros es que nuestras explicaciones son mucho más sencillas de formular y que la máquina nos escucha necesariamente sin hacer nunca lo que ella quiera y, sobre todo, lo entiende perfectamente a la primera.

Las pruebas y condiciones representan una idea básica muy simple para guiar nuestro programa: elegir ejecutar una instrucción determinada en función de la validez de una condición. De esta manera, comprobamos la validez de una condición para dar permiso o no para seguir ejecutando el programa, por ejemplo: si el semáforo de peatones está en verde (condición), entonces cruzo (instrucción).

La prueba también puede contener una o más alternativas: si el semáforo de peatones está en verde (condición), entonces cruzo (instrucción), de lo contrario espero a que el semáforo de peatones se ponga en verde.

Cuando se habla de condición, en realidad se está hablando valor buleano. Los buleanos son los tipos más sencillos de la informática. Solo pueden recibir dos valores: VERDADERO o FALSO. por tanto, la relación entre una condición y un buleano es totalmente explícita, porque una condición siempre es una expresión buleana.

Una condición siempre es el resultado de una o varias comparaciones...

1. Condiciones múltiples

Escribir una condición que compruebe la validez de un único hecho es bastante lógico, incluso sencillo. La complejidad de las condiciones aumenta a medida que aumenta el número de hechos que hay que validar, ya sea en la vida cotidiana o en la informática.

Cuando ponemos a prueba múltiples condiciones como seres humanos, nuestros cerebros razonan tan rápido que no parece que estemos pensando o incluso resolviendo una ecuación. Pero en realidad sí lo estamos haciendo.

Volvamos al ejemplo del paso de peatones. Parece que es normal que, antes de cruzar un semáforo, se compruebe si el semáforo para peatones está en verde y también que ningún coche se salta el semáforo. Por tanto, está analizando dos condiciones y tiene la impresión de que está haciendo las dos cosas a la vez con una sola condición. Pero su cerebro recibe dos condiciones para comprobar, así que resuelve estas dos condiciones en una ecuación.

Como dijimos en el capítulo introductorio de este libro, es necesario describir todo a la máquina, paso a paso, no hay atajos. Así que necesitamos una forma sencilla de representar múltiples condiciones.

Para formular correctamente esta ecuación con varias condiciones, George Boole, matemático del siglo XIX, creó un álgebra binaria que Claude Shannon utilizó más de un siglo después en informática. El álgebra de Boole, también llamada lógica de Boole según el contexto, permite analizar varias condiciones a la vez en una misma ecuación y, por tanto, en una misma estructura condicional. Así que ya sabe de dónde viene el nombre de Buleano.

Implementar esta álgebra es casi natural en informática. Un ordenador funciona con impulsos eléctricos, por lo que FALSO se representa por 0 o ausencia de corriente, y VERDADERO por 1 o presencia de corriente.

Este proceso de cálculo da prioridad a unas condiciones sobre otras, en función de los operadores elegidos.

2. Álgebra o lógica buleana

La lógica buleana se basa en tres operadores: Y, NO y O y dos valores: VERDADERO y FALSO.

Con estos tres operadores lógicos, podemos decirle al ordenador cómo resolver correctamente múltiples...

1. La importancia de la indentación

Python es un lenguaje con una sintaxis bastante particular que exige rigor por parte del desarrollador. Este rigor permite aligerar la sintaxis de Python y forzar buenas prácticas de desarrollo.

En Python, el código que no está indentado no se puede ejecutar por el intérprete.

Un script de Python se divide en bloques. Cada bloque se debe indentar con una nueva tabulación, como se muestra en la siguiente figura. Para volver al bloque anterior, basta con quitar un tabulador de las instrucciones. Para indicar al intérprete que un bloque está comenzando, la instrucción debe terminar con el carácter ":".

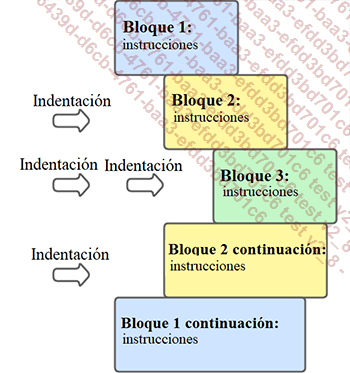
Indentación con Python

La regla es sencilla: un bloque de instrucciones = una indentación.

¿Por qué hablamos de esta regla? Simplemente porque una estructura condicional en Python se debe representar por un bloque. Al igual que Python utiliza un salto de línea para terminar una sentencia, utiliza un bloque para una sentencia condicional.

2. Visibilidad de las variables

Esta noción de bloque significa que tenemos que fijarnos en la visibilidad de las variables, también conocida como ámbito.

Las variables de un algoritmo se pueden utilizar en cualquier línea porque todas son conocidas a lo largo del algoritmo gracias a su declaración en el bloque VAR al principio del algoritmo. Estas variables se conocen como variables globales.

En Python, las variables se pueden declarar en cualquier momento, a diferencia de los algoritmos. Por lo tanto, las variables no son globales, sino locales al bloque en el que se declaran. Una variable declarada en el bloque 1 de la siguiente figura, se puede consultar en todos los bloques anidados dentro de él. Sin embargo, a una variable declarada en el bloque 2 solo pueden...