Ediciones ENI Editorial | líder en informática
Iteración
Introducción
Un tratamiento iterativo es un tratamiento que se repite, según el Diccionario de la lengua española. Este término es sinónimo de frecuentar, que se define como repetir un acto a menudo, como parpadear (...). En este capítulo construimos algoritmos de transformación durante los cuales el sistema pasa del estado inicial al estado final atravesando una sucesión finita de estados caracterizados por una propiedad común. Vamos a ver cómo construir este tipo de algoritmos de una manera razonada y sistemática.
La sección «Mis primeros ejemplos de construcción de iteraciones» introduce el método usando ejemplos sencillos. La sección «Iterar en una tabla» estudia distintas situaciones donde la iteración se utiliza con los componentes de una tabla. La sección «¿Algoritmo o programa?» es una explicación que justifica el método estudiado en el libro y propone ejercicios de aplicación durante los cuales se hace posible dar soluciones iterativas a ejercicios que, a veces, ya hemos resuelto con anterioridad. El capítulo termina con algunas notas bibliográficas y un resumen.
Mis primeros ejemplos de construcción de iteraciones
Estos ejemplos son sencillos. El primero, la construcción de una tabla de multiplicar, es incluso trivial. Se trata de una primera presentación para introducir los razonamientos que permiten construir una iteración: hay que evitar multiplicar las dificultades. Por eso empezamos centrándonos en las etapas de la construcción y del razonamiento para un problema elemental. El segundo ejemplo explora una tabla donde los datos son instancias de un tipo estructurado. La sección termina después con algunos ejercicios de aplicación de la misma naturaleza.
1. La tabla de multiplicar
a. El problema
Queremos preparar un algoritmo que llena una tabla con los resultados de la tabla de multiplicar de un número entero n positivo o nulo. Se trata de preparar una solución que presenta las etapas del cálculo de los elementos de la tabla. Esta tabla está limitada a 11 celdas, numeradas de 0 a 10, pero podría tener muchas más celdas sin modificar el algoritmo propuesto. Vamos a verlo.
La tabla de los resultados que deseamos obtener es:
...
constante
MIN: ENTERO 
0 # Número de la primera celda de la tabla
MAX: ENTERO 10 # Número de la última celda
variable
tabla: TABLA[ENTERO][MIN, MAX]
... Estas instrucciones declaran una tabla llamada tabla que contendrá MAX - MIN + 1 enteros, entre las celdas de números MIN y MAX. Para llenar tabla con la tabla de multiplicar del 4, por ejemplo, escribiremos:
...
tabla_de(tabla, 4)
... Falta definir el algoritmo del procedimiento tabla_de que inicializa esta tabla. Es un procedimiento que toma como entrada un número entero natural n y que inicializa una tabla que contiene los resultados de la tabla de multiplicar de n. Se define de la siguiente manera:
|
Algoritmo 1: Tabla de multiplicar - Versión 1.0 |
Algoritmo tabla_de
# La tabla de multiplicar de 'n'.
Entrada
t: TABLA[ENTERO] # La tabla a inicializar
n: ENTERO # El número entero para...Explorar una tabla
Un CLIENTE es una PERSONA identificada por un número entero. Una PERSONA tiene una DIRECCIÓN y una IDENTIDAD. El diagrama que aparece aquí debajo representa estas entidades y sus asociaciones mutuas.
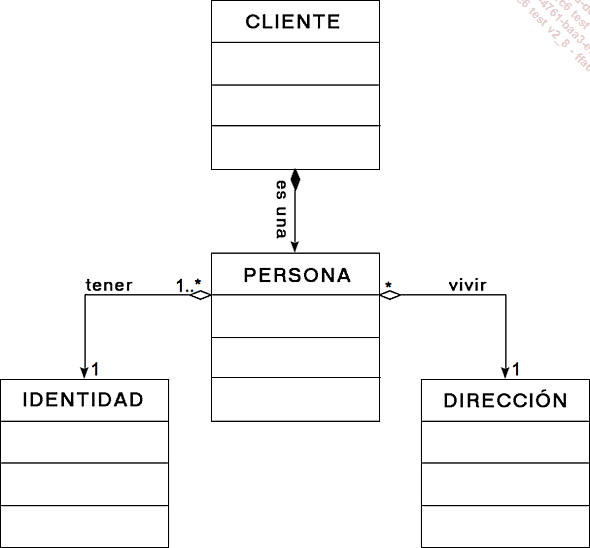
Observe la naturaleza específica de la asociación entre CLIENTE y PERSONA. De esta manera se indica que una instancia de CLIENTE está compuesta de una, y solo una, instancia de PERSONA. En sentido estricto, aquí habría que usar la asociación de herencia, pero no estamos en algoritmia de objetos. Además, el color del rombo del lado CLIENTE indica que, cuando el cliente desaparece, la persona desaparece con él. La explicación sobre las distintas asociaciones y su significado ya se mencionó en el capítulo «Estructuras elementales», en la solución del ejercicio n.º 11, en los elementos disponibles para descargar desde la página Información.
El tipo CLIENTE se define mediante la declaración:
tipo
CLIENTE
estructura
número: ENTERO
p : PERSONA
fin CLIENTE La declaración del tipo PERSONA es similar:
tipo
PERSONA
estructura
identidad: IDENTIDAD
edad : ENTERO
dirección: DIRECCIÓN
fin PERSONA Por último, el tipo DIRECCIÓN ya se ha utilizado en el capítulo «Estructuras elementales».
Se ha declarado e inicializado una tabla que puede contener hasta 1000 CLIENTES:
constante
MAX_CLIENTES: ENTERO 1000
MIN_CLIENTES: ENTERO 1
VACÍO: ENTERO ??? # Número de un cliente que no existe
BORRADO: ENTERO ??? # Número de un cliente borrado
...
variable
clientes: TABLA[CLIENTE][MIN_CLIENTES, MAX_CLIENTES]
... En este momento, todas las celdas no han sido necesariamente inicializadas por clientes. Quizás la empresa todavía no tiene 1000 clientes. La primera celda que todavía no se ha inicializado lleva un número...
¿Algoritmo o programa?
Ahora sabemos lo suficiente para volver sobre algunos conceptos que ya se han explicado en los capítulos «¿Qué es la algoritmia?» y «Programas directos». ¿Qué es un algoritmo?, ¿qué lo distingue de un programa destinado a un ordenador? Construir un programa y definir un algoritmo son actividades distintas, cada una desarrolla sus propios métodos ¿o solo son las «dos caras de la misma moneda»? Esta sección no busca responder de manera definitiva. Solo se exponen algunas ideas sencillas que completan la visión parcial de los capítulos anteriores. La primera parte desarrolla un ejemplo copiado de un libro de algoritmia. La segunda parte expone una de las soluciones recomendadas para el problema.
1. Un ejemplo edificante
Se ha inicializado una tabla de nombre marcas de 100 componentes reales positivos con n números, 0 ≤ n ≤ 100, para los que queremos determinar la media aritmética. En un libro que no voy a citar, leo la siguiente solución:
VAR
marcas : TABLA[1 .. 100] de REAL;
números: ENTERO;
suma, i: ENTERO;
media : REAL ;
INICIO
(* Llenar la tabla *)
i:= 1;
escribir("Dar un número entero: ");
leer(marca[i]);
MIENTRAS(marcas[i] < > - 1)
INICIO
i:= i + 1;
escribir("¿Cuál es el número entero siguiente?") ;
leer(marcas[i]);
FIN;
(* Calcular la media *)
números:=i ;
i:= 1;
suma:= 0;
MIENTRAS(i < > números)
INICIO
suma:= suma + marcas[i];
i:=...Ejercicios de aplicación
Esta sección propone ejercicios de aplicación variados. El primero amplía el estudio iniciado en el capítulo «Estructuras elementales».
|
Ejercicio 6: Historial de una cuenta corriente |
Se quiere conservar el historial de los movimientos mensuales en una cuenta corriente.
1. Modificar el tipo CUENTA definido en el capítulo «Estructuras elementales» para conservar el rastro de los movimientos en una cuenta durante un mes.
2. Establecer el saldo a final de mes de una cuenta dada.
El saldo ya no es un atributo de la cuenta. Se obtiene recorriendo el historial mensual y anual que registra el importe del saldo de la cuenta para cada mes.
3. Rehacer las definiciones anteriores.
Una tabla clientes contiene las cuentas corrientes de un conjunto de clientes.
4. Determinar los clientes para los que la media de los importes de los movimientos es superior a una suma dada.
El ejercicio siguiente se resolverá por completo en el capítulo «Edición de un número».
|
Ejercicio 7: Edición de un número entero |
1. Escribir un algoritmo iterativo que transforme un número entero n cualquiera en su representación en una base B ≥ 2 cualquiera.
Cuando la base es superior a 36, se puede utilizar la representación de los números en base diez, pero separando cada cifra de la representación del número en base B mediante un separador convenido, por ejemplo, un punto. Eso es lo que se usa para expresar, por ejemplo, la dirección IP de un host en una red con IPv4. Así, por ejemplo, la representación en base 256 de 3000, expresada aquí en base diez, se escribirá: 11 184256 = 3000diez.
Este ejercicio está completamente resuelto en el capítulo «Edición de un número».
|
Ejercicio 8: Análisis de una cadena de caracteres |
Sea una cadena de caracteres con distintas partes separadas por un carácter SEPARADOR específico. El ejemplo que aparece aquí debajo representa una cadena de este tipo, donde el carácter separador es dos puntos ’:’.
Este es un:ejemplo : de cadena a analizar: Se quieren separar las distintas partes y situarlas en una tabla de cadenas de caracteres. Para el ejemplo...
Resumen
En este capítulo hemos visto la construcción razonada de una iteración. Una iteración es un tratamiento repetido en un conjunto de datos que evolucionan, pero quedan vinculados mediante condiciones estrictas. Construir la iteración es formular claramente la hipótesis de recurrencia subyacente para deducir los tratamientos que garantizan los cambios de estado del sistema, las inicializaciones que realizan el estado inicial, la condición de terminación que describe el estado final, el invariante que enuncia una propiedad cuyos tratamientos, en todos los estados del sistema, garantizan la permanencia y el invariante de control que es una medida de la distancia al estado final. Los ejemplos propuestos han mostrado cómo construir una iteración según este «modelo». Se han tomado prestados de distintos campos, pero no llaman a otras estructuras de datos que no sean la tabla simple o la cadena de caracteres.
Los capítulos siguientes solo son variaciones sobre el tema de la construcción de una iteración y de la especificación de un algoritmo.