Encriptar

1. Presentación

Los datos que nos interesan «contienen» una cierta «información». Cualquier perturbación de los datos modificará esta información.

Las perturbaciones pueden ser de distinta naturaleza. Así, por ejemplo, en el momento de escribir o leer hacia o desde un disco, el entorno electromagnético del sistema puede modificar los datos de una manera imprevisible durante su transferencia. Igualmente, durante un intercambio de datos a través de una red, un usuario puede interceptar y modificar los mensajes de una manera ilegítima o inesperada. Una aplicación puede corromper los datos con los que trabaja, como consecuencia de un incidente de funcionamiento, por ejemplo.

Los métodos habituales que nos interesan en esta sección permiten asegurarse de que los datos conservan «la información que contienen». Así, queremos convencernos de que los datos no han sufrido modificaciones. Entonces se trata de garantizar la integridad de los datos utilizados. El principio general de este tipo de método se ilustra mediante la figura siguiente.

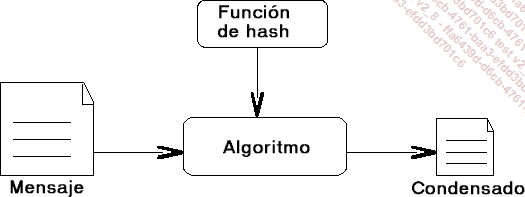
Un algoritmo calcula un condensado o huella (hash) del mensaje. Sea cual sea el tamaño del mensaje, el condensado tendrá una longitud fija, por ejemplo, de 32 bytes (256 bits). Así, toda la información contenida dentro del mensaje estará comprimida, «condensada» en 32 bytes.

Para asegurarnos de que los datos no han sufrido perturbaciones, se recalcula, con el mismo algoritmo, el condensado del mensaje que se ha de verificar y se compara con el condensado original. A continuación se detallan las operaciones:

Este método se ilustra mediante la siguiente figura.

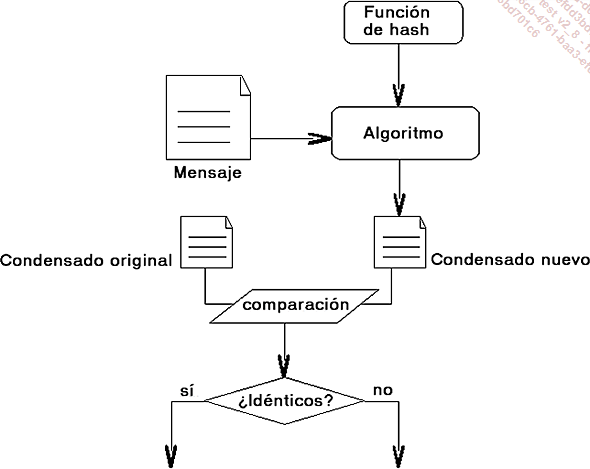
En esta figura, el condensado original es el condensado enviado por el emisor y recibido por su destinatario con el mensaje. El condensado nuevo es la huella calculada por el receptor del mensaje. Aseguramos que el mensaje no ha sufrido modificaciones cuando el condensado nuevo calculado es idéntico al condensado recibido. Sin embargo, está claro que la cantidad de huellas distintas es finita, exactamente 2²⁵⁶ para una huella de 32 bytes, mientras que la cantidad de mensajes...

1. Principios matemáticos de la confidencialidad

Sean M el conjunto de los mensajes sin codificar, C el conjunto de los mensajes encriptados y K el conjunto de las claves de cifrado. La operación de cifrado es una función S de M x K en C:

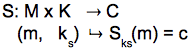
El descifrado es una función D de C x K en M :

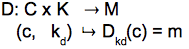
Las claves de cifrado/descifrado son k_s y k_d, respectivamente. Las dos funciones verifican: D_kd(S_ks(m)) = m. Esta fórmula expresa que el cifrado es reversible. Estas operaciones se pueden representar como en el dibujo de la figura que aparece a continuación.

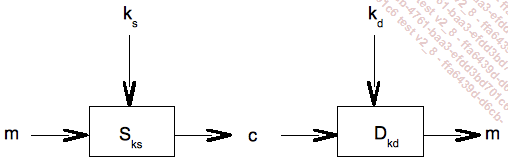
Los algoritmos de cifrado usan distintas relaciones recíprocas entre k_s y k_d.

2. Criptografía con clave secreta

Cuando existe un medio sencillo de obtener k_d a partir de k_s, se habla de cifrado simétrico o también de cifrado con clave secreta. En este caso, las dos extremidades comparten un secreto común. Este puede ser, por ejemplo, el mismo valor de clave k = k_s = k_d. Entonces, toda entidad que conoce k puede descifrar el mensaje c para obtener el mensaje m.

En teoría, sabemos garantizar una confidencialidad perfecta con este tipo de encriptado, donde las entidades que se comunican comparten un secreto común. Sin embargo, esta confidencialidad perfecta solo se obtiene pagando el precio de condiciones previas irrealizables. El algoritmo de Vernam es especialmente sencillo y garantiza el secreto perfecto des los intercambios en estas condiciones. Vamos a verlo.

Sean A y B, como Alicia y Bob, por ejemplo, las dos entidades que comparten una clave común k. Esta clave es una serie aleatoria de bits de la misma longitud que el mensaje m que se ha de enviar. Para encriptar el mensaje, A utiliza la función S_k = m  k, donde designa al operador booleano O EXCLUSIVO. Habitualmente, este operador se expresa como , pero hemos usado este último símbolo para representar la concatenación de las cadenas de caracteres y seguiremos haciéndolo. Como la función S_k es una involución, B usa D_k = c  k para encontrar m. El secreto perfecto exige que el número de claves...