Usar varias capas de neuronas
Lo que vamos a descubrir y requisitos
En el capítulo anterior hemos descubierto el funcionamiento de una neurona normal y ahora vamos a concentrarnos en las redes neuronales multicapa.
Requisitos necesarios para abordar este capítulo correctamente: haber leído los capítulos Los fundamentos del lenguaje Python, Estadísticas para comprender los datos, Principales algoritmos de Machine Learning y La predicción con neuronas.
Funcionamiento de las redes neuronales multicapa
El funcionamiento de una neurona formal es bastante fácil de comprender con la ayuda de conceptos como neuronas de entrada, pesos, sesgo y una función de activación. El objetivo de esta neurona es minimizar su función de costes aprendiendo de sus errores. En el capítulo anterior hemos insistido mucho sobre el hecho de que una neurona formal solo es capaz de clasificar datos linealmente separables, pero en la práctica es muy raro que los datos sean de este tipo. Por eso han aparecido las redes neuronales multicapa.
Su funcionamiento es idéntico al de la neurona formal. Por eso, recuperaremos las acciones de propagación y de retropropagación que se aplican a todas las capas de la red. La función de activación solo se aplica a las neuronas encargadas de realizar la clasificación.
OR exclusivo (XOR)
Haga memoria: hemos visto que, cuando utilizamos la función lógica OR exclusivo, también llamada XOR, los datos no son linealmente separables. En efecto, hay dos rectas de separación y no una sola. Por lo tanto, una sola neurona no puede tener éxito clasificando los datos.
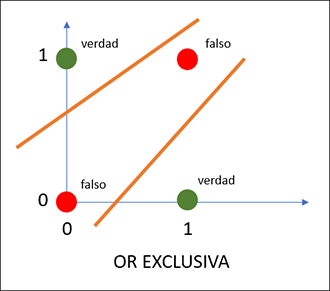
Representación gráfica de la función lógica OR Exclusivo
1. ¿Cuántas capas y neuronas necesitamos?
Sabemos que una neurona formal tiene la facultad de clasificar los datos en dos clases. En el caso de XOR, tenemos que hacer dos separaciones de dos clases (dos rectas). Por eso necesitaremos una capa adicional como mínimo.
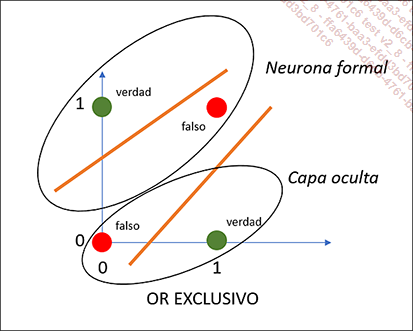
Cantidad de capas de neuronas necesarias
Ahora podemos modelizar nuestra red de neuronas como se indica en la figura siguiente, mostrando las neuronas de entrada, la capa oculta y la neurona de salida, sin olvidar los sesgos. Todas las neuronas están conectadas unas con otras; por eso decimos que nuestra red está «completamente conectada» (Full connected).
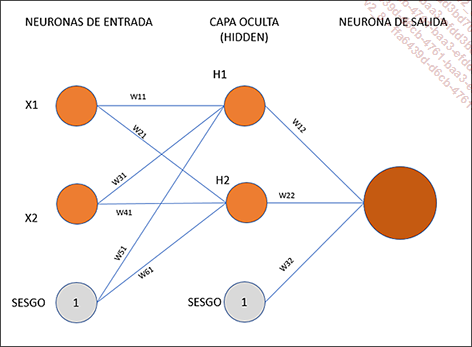
Redes de neuronas multicapa
2. Un ejemplo numérico
La programación de estas redes no es muy compleja; las etapas que hay que seguir se corresponden con las de la neurona formal:
-
Initialización de los pesos.
Cálculo de la preactivación.
Activación.
-
Cálculo del error.
Retropropagación (actualización de los pesos de cada capa).
a. Datos de aprendizaje
La tabla que aparece aquí debajo retoma los distintos resultados relacionados con la lógica de OR Exclusivo respetando las siguientes normas:
-
El resultado es VERDAD si uno y solo uno de los operandos A y B es VERDAD.
-
El resultado es VERDAD si los dos operandos A y B tienen valores distintos.
-
El resultado es VERDAD si una cantidad impar de entradas es verdad.
|
OR EXCLUSIVO (XOR) |
||
|
A |
B |
A XOR B |
|
0 |
0 |
FALSO |
|
0 |
1 |
VERDAD |
|
1 |
0 |
VERDAD |
|
1 |
1 |
FALSO |
b. Inicialización de los pesos
Ahora vamos a inicializar de manera aleatoria los pesos en el intervalo [-1 y 1] y dar el valor 0 a los sesgos:
W11 = -0,165955990594852,
W21 = 0,4406489868843162,
W31 = -0,9997712503653102,
W41 = -0,39533485473632046,
Capa oculta
W12 = -0,7064882183657739,
W22 = -0,8153228104624044,
Sesgo
W51 = 0,
W61 = 0,
W32 = 0, c. Carga de los datos de entrada
Ahora cargamos...
Vuelven las minas y las rocas
Haga memoria: en el capítulo Clasificar bien no es una opción, tratamos el caso de la clasificación de un objeto como una mina o una roca en función de las mediciones efectuadas por un sonar.
Este caso de estudio también se trató en un artículo titulado «Analysis of Hidden Units in a Layered Network Trained to Classify Sonar Targets» («Análisis de unidades ocultas en una red multicapa entrenada para clasificar objetivos de sonar»), escrito por Terry Sejnowski y R. Paul Gorman en 1988. Su objetivo era demostrar la importancia del papel de la cantidad de neuronas en la capa oculta sobre la precisión de clasificación.
Por supuesto, este estudio se puede descargar en la web, pero hemos puesto una copia a su disposición dentro de la carpeta destinada al código de este capítulo, que puede descargarse desde el sitio del editor.
Ahora vamos a ver los distintos parámetros utilizados por estos dos científicos para realizar su demostración:
-
192 datos de aprendizaje.
-
16 datos de pruebas.
-
60 neuronas de entrada (correspondientes a cada una de las frecuencias).
-
2 neuronas de salida (una por la probabilidad correspondiente a una mina y otra por la probabilidad correspondiente a una roca).
-
300 epochs.
-
Una tasa de aprendizaje de 2,0.
-
Pesos inicializados en el intervalo de valores comprendidos entre -0,3 y 0,3.
-
Una actualización de los pesos solo en caso de que el valor predicho difiera más o menos 0,2 con el esperado.
-
Uso de una función de activación de tipo sigmoide.
-
Una capa de neuronas compuesta de 0, 2, 3, 12 o 24 neuronas.
En este capítulo vamos a intentar conseguir los resultados que obtuvieron durante el estudio, pero nosotros también trataremos de demostrar que la cantidad de neuronas en una capa oculta influye sobre la precisión de la clasificación.
1. ¿Más neuronas en la capa oculta dan lugar a mejores resultados?
Antes de seguir, le invitamos a crear un proyecto de Python nuevo con una carpeta datas donde colocaremos los datos de las observaciones que ya utilizamos en el capítulo Clasificar bien no es una opción.
a. Carga de datos de aprendizaje
Una vez hecho esto, podemos cargar las observaciones de la siguiente manera:
#---------------------------------------------
# CARGA DE LAS OBSERVACIONES ...Conclusión
En este capítulo hemos visto el principio de funcionamiento de las redes neuronales multicapa que nos permiten clasificar datos que no son linealmente separables.
También hemos podido validar la afirmación de Terry Sejnowski y R. Paul Gorman, según la cual la cantidad de neuronas presentes en la capa oculta influye en el resultado de la clasificación. Igualmente podemos constatar que hemos conseguido un resultado de clasificación mejor que el obtenido en el capítulo Clasificar bien no es una opción o el del algoritmo máquina de vectores de soporte, donde la precisión no sobrepasaba el 89 %.
Pero, no obstante, es conveniente asegurarse de que el modelo pueda generalizarse evaluando la desviación entre la precisión obtenida con los datos de aprendizaje y la que se obtiene con los datos de pruebas.
En el capítulo siguiente vamos a abordar el campo de la clasificación de imagen con ayuda de otro tipo de redes neuronales, denominadas redes neuronales convolucionales.
 Ediciones ENI Editorial | líder en informática
Ediciones ENI Editorial | líder en informática



